Kinematics in circular motion
Torque
rotational motion
Rotational Inertia
Newtons 2nd law in rotational form
100
what is one of the three rotational kinematic equations.
Δω = αΔt
ωf = ωi + α(tf - ti).
100
What is Torque
Torque (τ) is the rotational equivalent of force, causing an object to rotate about an axis.
100
If the gravitational force between the Earth and the Sun were to stop acting, which of the following statements best describes the resulting motion of the Earth?
(a) It would continue revolving around the Sun and rotating on its axis.
(b) It would continue rotating on its axis but stop revolving around the Sun.
(c) It would stop rotating on its axis but continue revolving around the Sun.
(d) It would stop revolving around the Sun and rotating on its axis.
(b) It would continue rotating on its axis but stop revolving around the Sun.
100
What does moment of Inertia stand for
Moment of inertia (I) represents an object's resistance to rotational motion, dependent on its mass distribution
100
What is Newton's 2nd law formula for rotational motion.
∑τ = Iα
∑τ = dL/dt
200
A disk is free to rotate about a central axis. The graph below shows the disk's angular velocity as a function of time.
Which statements are true for the time interval represented on the graph?
(a) The disk's angular displacement is 50 rad
(B) The disk spins in only one direction throughout the time interval.
(C) The disk's angular acceleration is 5 rad/s^2
(D) The disk's initial velocity is 10 rad/s
(a) and (b)
200
What is the rotational analogue of force?
(a) Torque
(b) Inertia
(c) Momentum
(d) Power
(a) Torque
200
The disk below rotates about an axis that passes through its center, at Point I. The axis of rotation sticks out of the screen.
What is the correct relationship between the angular speeds, ω, of points II, III, and IV on the disk?
ω II = ω III = ω IV
200
A skier is testing different skis. He first uses skis with length L and mass M.
For his next run, the skier wants skis that are easier to maneuver and turn quickly.
Which skis could he use to achieve the desired behavior?
Assume the density of a given pair of skis is uniform.
Skis with the same length L and mass less than M
or
Skis with the same mass M and length less than L
200
A double pulley is free to rotate as one rigid system about an axis through its center. The radii of the two pulleys are \[R\] and \[2R\]. Two strings are wrapped in opposite directions around the pulleys. A mass hangs from each string. The two tension forces act on the pulley as modeled below, with \[F_1 = F_2\].
When released from rest, what will be the direction of the pulley's angular acceleration?
clockwise
300
A merry-go-round is rotating with an angular velocity of 11.4 rpm (revolutions per minute) counterclockwise. At the end of the ride the brakes are applied, giving the merry-go-round a constant angular acceleration of 0.083 rad/s^2 clockwise as it slows to a stop.
How much time does it take the merry-go-round to slow to rest?
Round your answer to the nearest second.
14s
300
A Ferris wheel is modeled below. Passenger cabins hang from the wheel at rest. Four of the cabins are labelled. Assume all of the cabins are empty and have the same mass.
From greatest to least, rank the torque magnitudes resulting from each cabin hanging on the wheel.
D < A < B < C
300
A wind turbine is modeled below. The tip of each blade is a distance r from the central axis of rotation. The turbine rotates at a constant angular speed ω for a time interval Δt.
Derive an expression for the linear distance travelled by one of the blade tips during the time interval Δt.
rωΔt
300
A rigid object is subjected to a net external torque. What quantity describes the object's resistance to changes in its rotational motion?
(a) Angular velocity
(b) Angular acceleration
(c) Rotational inertia
(d) Kinetic energy
(c) Rotational Inertia
300
A mass is attached to a string that's wrapped around a pulley at rest. The pulley has a rotational inertia of \[0.75\text{ kg}\!\cdot\!\text{m}^2\] and is free to rotate about an axis through its center. Friction between the pulley and axle is negligible. At time \[t = 0\] the mass is released and allowed to fall, rotating the pulley. The resulting torque on the pulley is \[3.0\,\text{N}\!\cdot\!\text{m}\].
What is the pulley's angular speed after \[1.8\,\text{s}?\]
Enter your answer with two significant figures.
7.2 rads/s
400
At 12:20 PM, an analog clock is in the configuration shown below.
What is the angular displacement Δθ of the clock's minute hand from 12:20 PM to 2:30 PM?
Assume Δθ does not reset to zero after each revolution.
(13π/3) rad
400
A lunchbox lid is free to rotate about one of its ends. The lid has length L and mass m. At the instant modeled below, the lid is 30^degree above the horizontal.
Which expression represents the torque magnitude the lid experiences from gravity at this instant?
Assume the lid has uniform density.
(mgL/2)sin60^degree
400
A car has four wheels. Each wheel, including its tire, has a diameter of 0.60 m as modeled below.
The car moves in a straight line while the driver applies the brakes. A graph of the wheels' angular velocity as a function of time during the braking period is shown below.
What distance did the car travel during the time represented on the graph?
(Do not round)
45 m
400
A flat metal triangle has three holes, labelled below. Inserting a nail through a hole allows the triangle to rotate about an axis passing through that hole.
Rank the rotational inertia of the triangle as it rotates about the different axes.
Assume the triangle has uniform density, and that the holes represent a negligible loss of mass.
I_\text{A}>I_\text{C}>I_\text{B}
400
A meterstick with uniform density rests on a horizontal surface with negligible friction. Two forces are applied to the meterstick parallel to the surface. A top-down diagram of these forces is shown below, along with a coordinate system.
Top-down view of a meterstick. The meterstick rests flat on a surface and is not fixed at any point.
Complete the statement about static equilibrium.
A third force can be applied to the meterstick to establish static equilibrium. This force should have a magnitude of
, act in the
direction, and be applied at location
.
answer
500
A ceiling fan is free to rotate about a central axis. The graph below represents the fan's angular acceleration as a function of time.
Which of the following graphs of angular velocity as a function of time could represent the fan during the same time interval shown above?
500
A wrench is used to turn a bolt. The wrench rotates clockwise around an axis of rotation passing through the center of the bolt. Two possible forces that could be applied to the wrench are modeled below.
Force A results in a torque of magnitude τ A about the axis of rotation. Compared to force A, force B has one-half the magnitude and acts twice as far from the axis of rotation.
What torque magnitude results from force B?
TA/2
500
A belt drive is modeled below, consisting of two pulleys connected by a belt. The small pulley is rotated by a motor. Static friction between the belt and pulleys prevents the belt and pulleys from slipping past each other. So, the small pulley's rotation causes the belt to move, which causes the large pulley to rotate.
The large pulley has a radius of 0.20 m and is initially at rest. When the motor is switched on, the large pulley undergoes a constant angular acceleration of magnitude 2 rad/s^2.
Find the linear speed of a point on the belt after 4.0s.
(Round your answer to the nearest tenth).
1.8 m/s
500
A playground merry-go-round rotates about an axis of rotation that passes through its center. A child and adult are sitting on the merry-go-round. The system consisting of the merry-go-round, the child, and the adult is modeled below in four different configurations.
From greatest to least, rank the configurations by their total rotational inertia, \[I_\text{tot}.\]
Assume the adult is more massive than the child. Also assume that friction between people and the merry-go-round prevents the people from sliding during rotation.
From greatest to least \[I_\text{tot}\] the answer is:
500
A disk is initially rotating clockwise around a frictionless axis with angular speed \[\omega_0\]. At time \[t=0\], the two forces of magnitude \[F_1= 25\,\text N\] and \[F_2= 25\,\text N\] are exerted on the disk as modeled below.
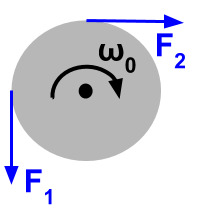
Which graph could represent the disk's angular velocity over time?
Consider counterclockwise the positive direction.
\[\omega\]\[t\]\[-\omega_0\]\[O\]
The disk's initial angular velocity is in the negative (clockwise) direction. The net torque on the disk is zero, which will cause zero angular acceleration (slope).