Performing Transformations
Describing Transformations
Transforming Points
Reflections of points
Rotation of points
100
When you reflect over the Y Axis it changes the ____?
X coordinate.
100
Is this a reflection or rotation?
No.
100
What are the coordinates of point (-5,-6) after a reflection over the Y-Axis?
(5,-6)
100
The image of P (-6, -9) is reflected over the x-axis.
image is P' (-6, 9).
100
Rotate P through 180° about the origin, the new position of points P is:
P (-3, 1) →
P (-3, 1) → P' (3, -1)
200
When you rotate 180 degrees what changes?
The signs of the x and y coordinates.
200
Describe the transformation:
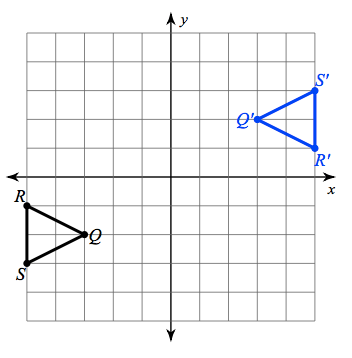
Rotation: 180° around (0,0)
200
What are the coordinates of point (-4,8) after a rotation of 180 degrees?
(4, -8)
200
The image of Q (5, 7) when reflected over the x-axis.
is Q' (5, -7)
200
Rotating M through 180° about the origin, the new position of points M is:
M (-2, 3) →
M (-2, 3) → M' (2, -3)
300
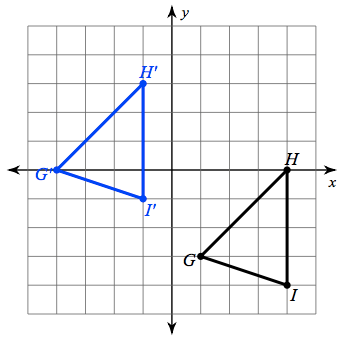
Rotate the triangle 90° clockwise around (0,0):
300
IS this a reflection?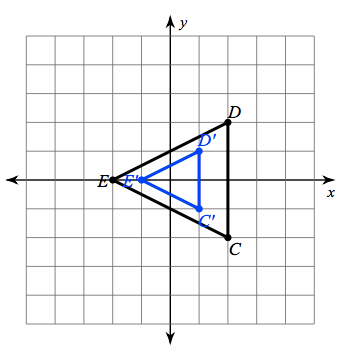
No.
300
What are the coordinates of point (8,-3) after a rotation 90° counterclockwise around the origin?
(3,8)
300
The image of R (4, 8) is reflected over the y-axis.
The image is R' (-4, 8).
300
When rotated through 90° about the origin in clockwise direction, the new position of the above points are;
point P (5, 7)
The new position of point P (5, 7) will become P' (7, -5)
400
Describe the transformation:
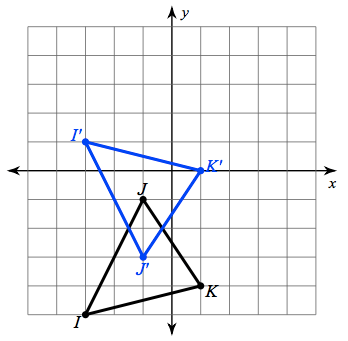
Reflection over y=-2
400
Point A (3,4) was reflected over the x-axis to Point A' (-3,4). What did they do wrong?
They should be changed, not the x. The point should be (3,-4)
400
The image of S (5, -7) over the y-axis.
The image becomes S' (-5, -7).
400
When rotated through 90° about the origin in clockwise direction, the new position of the above points are;
point Q (-4, -7)
The new position of point Q (-4, -7) will become Q' (-7, 4)
500
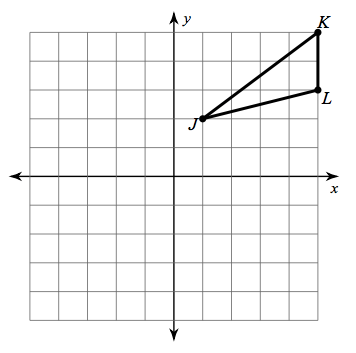
Reflect the triangle over the line y=1:
500
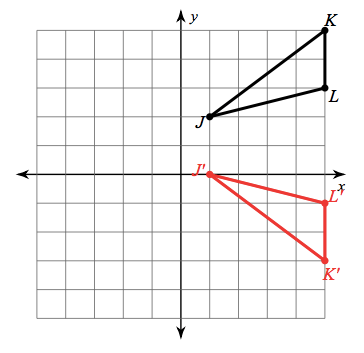
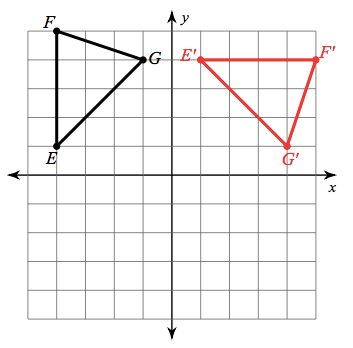
Which transformation is shown here?
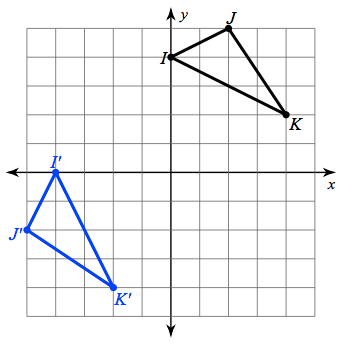
Reflection
500
After a transformation, the point A (-4,7) became the point A' (-4,-7).
Reflection over x - axis
500
What are the two things you need to remember to complete any reflection?
Over the y changes the x.
Over the x changes the y.
500
When rotated through 90° about the origin in counterclockwise direction. The new positions of the above points are:
point A (2, 3)
The new position of point A (2, 3) will become A' (-3, 2)