Random
Translations
Reflections
Identifying Rules
Recognize the transformation
100
212
441
100
Describe a translation
Moving all points in the figure the same distance and the same direction.
100
What happens to a coordinate when reflected over the x-axis?
Changes the sign of the y value.
100
Point D(-11, 2) is transformed and ends up at (-6, 4). What type of transformation ocured?
Translation
100
The graph depicts a rigid transformation. What is the rule? Give the words and the notation.
1 unit right 2 units down: (x + 1, y - 2)
200
Solve for x:
3x + 5 = 20
What is x = 5?
200
Adding to the x-coordinate moves a figure in this direction.
to the right
200
This value stays the same when a figure is reflected over the y-axis.
the y-value
200
An enlargement or reduction are examples of what type of transformation?
Dilation
200
The given graph depicts a rigid transformation.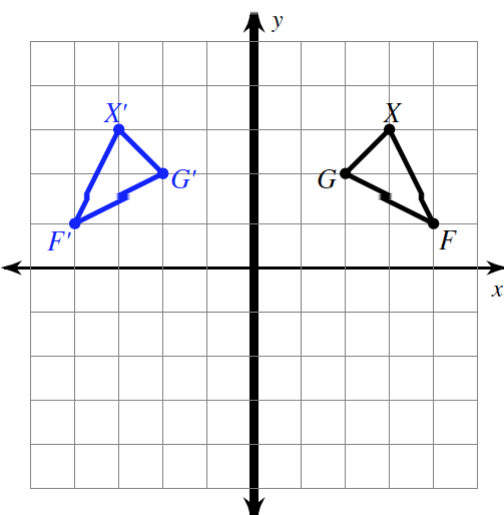
What is a reflection in the y-axis?
300
This type of relationship has a graph that is a straight line and passes through the origin.
What is a proportional relationship?
300
If (1, 6) is translated to the left 3 and down 1, what are the new coordinates?
(-2, 5)
300
Point (28, -37) is reflected over the y axis, then reflected over the x-axis. What is the coordinate of the Image?
(-28, 37)
300
If (1,5) becomes (3,0) what did we do to both the x and y value?
(x + 2, y - 5)
300
The given graph depict multiple transformations of the pre-image *. This image depicts a Reflection of * across the y-axis.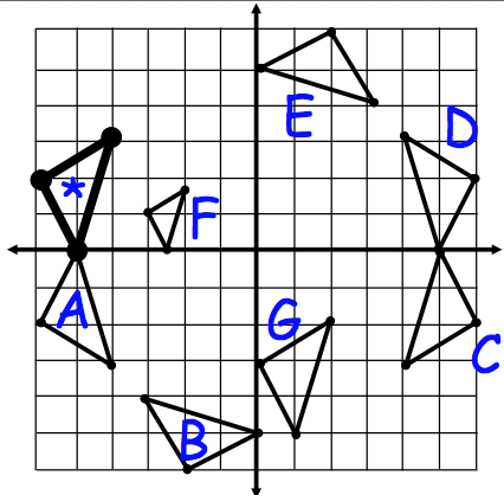
What is D?
400
The square root of 729.
What is 27?
400
Point K(-9, 13) is translated 9 units up and 13 units left. What is the coordinate of the image?
(0, 0)
400
The figure has been reflected over this line.
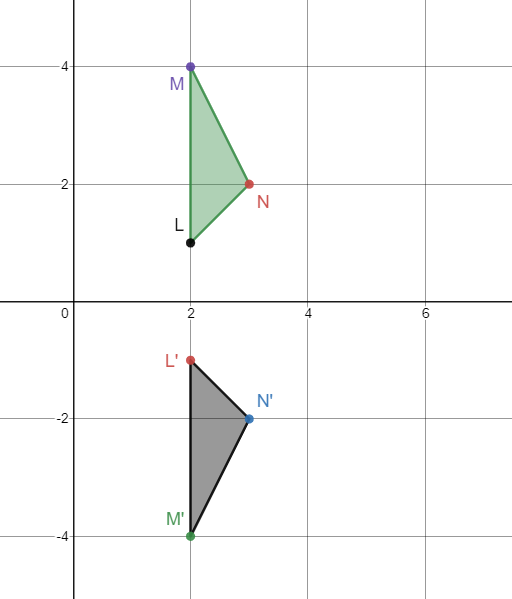
the x-axis
400
Define a reflection.
A reflection is a flip across the x or y axis
400
The given graph depicts a rigid transformation.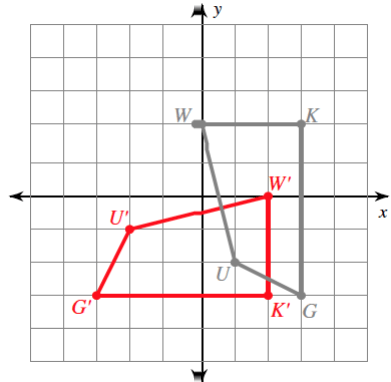
What is a 90-degree clockwise rotaition?
500
If a right triangle has legs of 7 cm and 24 cm, this is the length of the hypotenuse.
25 cm
500
In words, what is the translation rule for the figure to image below?
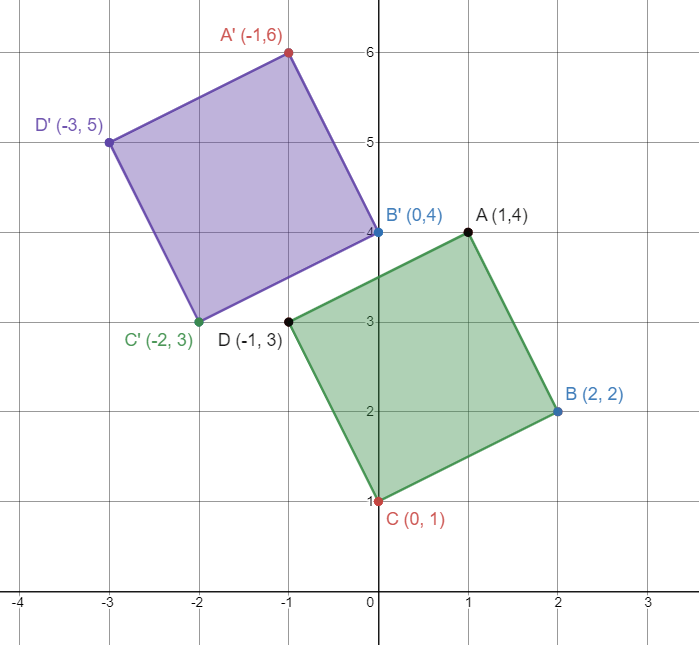
left two units, up two units
500
Reflect the triangle ABC over Y-axis with side lengths AB =3 units, BC = 4 units and AC = 5 Units. After reflection What is the length of BC?
4 Units.
500
Name the four types of Transformations.
Translation, reflections, rotations, dilations
500
The given graph shows rigid transformations of the pre-image . Triangle * will have a Rotations of 90-degrees counterclockwise about the origin. Where will the new figure be?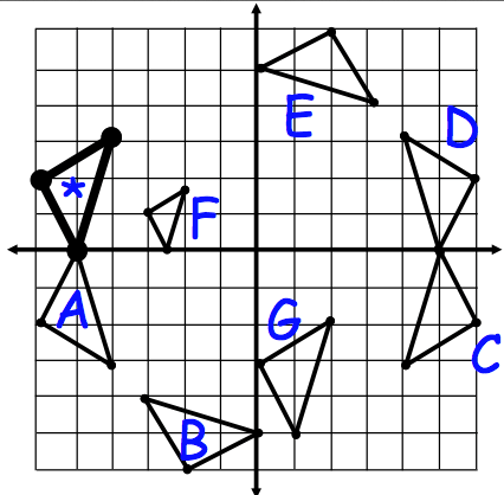 
What is figure B?