TRIPLE POINTS
Another word for translation.
Shift or Slide
Another word for rotation:
Turn
This word is another way of saying reflecting
Flip
This rule describe translating up 6 units.
(x, y+6)
TRIPLE POINTS
The graph depicts a rigid transformation. What is the rule? 
1 unit right 2 units down OR (x + 1, y - 2)
Adding to the x-coordinate moves a figure in this direction.
To the Right
If both coordinates change signs what transformation occurred? (-x,-y)
180 degree rotation
This coordinate stays the same when a figure is reflected over the y-axis.
the y-coordinate.
Describe this transformation rule: (x, y) maps to (x,-y)
reflection over the x-axis
The given graph depicts a rigid transformation.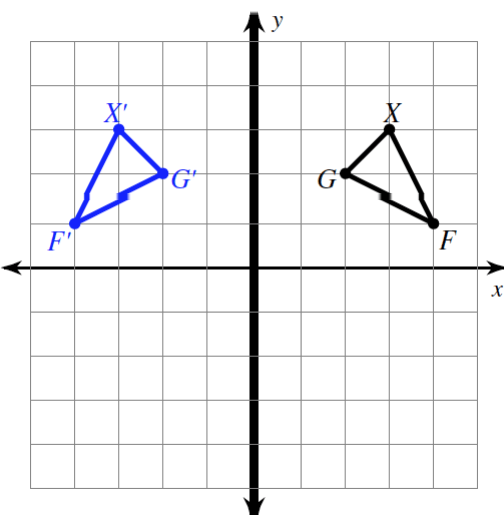
What is a reflection in the y-axis?
DOUBLE POINTS
Describe the rule for translating a figure 2 units up and 3 units to the left.
(x + 2, y - 3)
This is the coordinate M' after the figure below is rotated 180o clockwise.
(-6, -6)?
DOUBLE POINTS
The figure has been reflected over this line.

The X-axis
This rule describes rotating 270o clockwise.
(x,y) maps to (y,-x)
The given graph depicts a rigid transformation.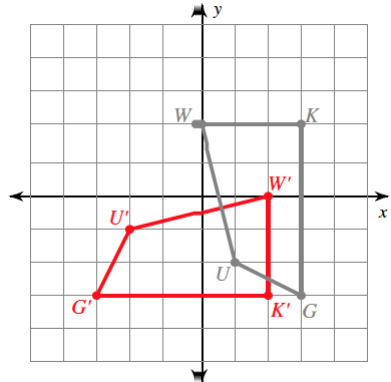
What is a 90-degree clockwise rotaition?
In words, what is the translation rule for the figure to image below?
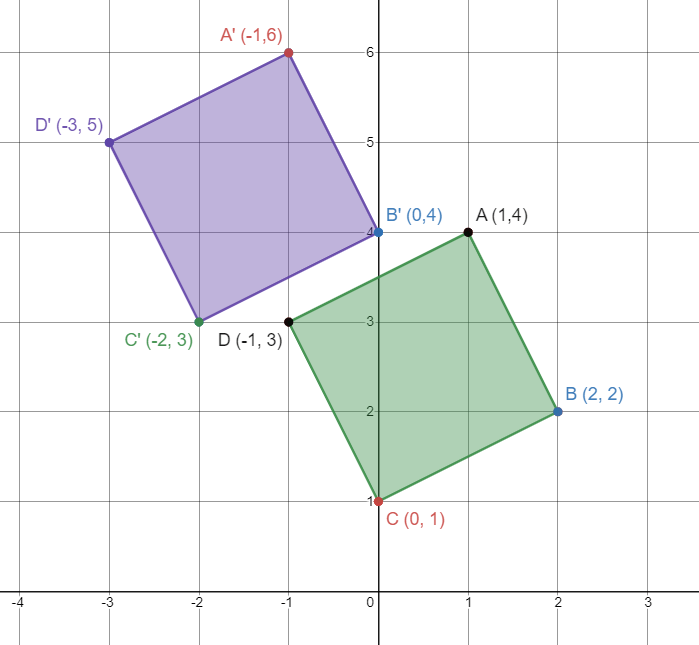
Left 2 units, Up 2 units
This clockwise rotation is the same as rotating 90o counterclockwise.
270o clockwise
Reflect the triangle ABC over Y-axis with side lengths AB =3 units, BC = 4 units and AC = 5 Units. After reflection What is the length of BC?
4 Units.
(x,y) maps to (-x,-y)
Rotation of 180 degrees
The given graph shows rigid transformations of the pre-image . Triangle * will have a Rotations of 90-degrees counterclockwise about the origin. Where will the new figure be? 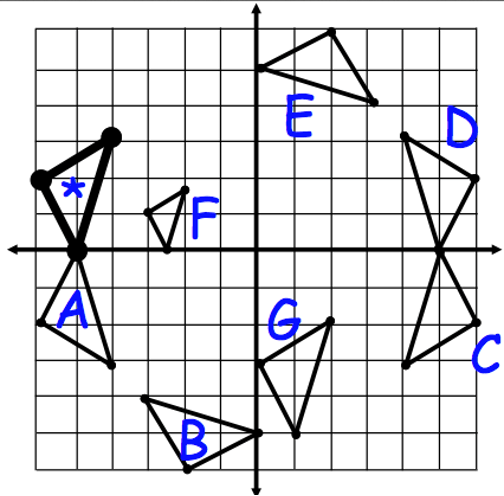
What is figure B?
Give the verbal description for the following transformation rule: (x - 4, y + 0)
Shift 4 units left
What would be the transformation in the illustration?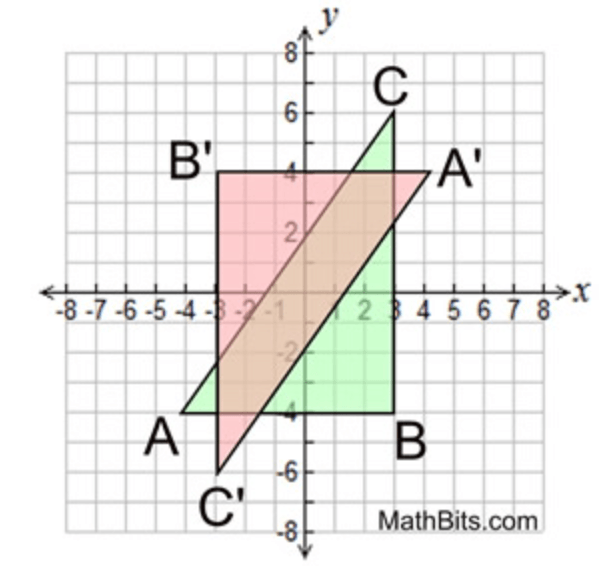
180 degree rotation
A reflection in the x-axis of the word WOW would produce this word.
MOM
DOUBLE POINTS
What is the rule for the given transformation: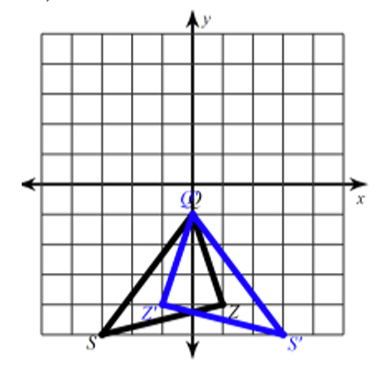
Reflection across the y-axis (𝑥, 𝑦) → (−𝑥,𝑦)
These two transformations have occurred to the given figure. 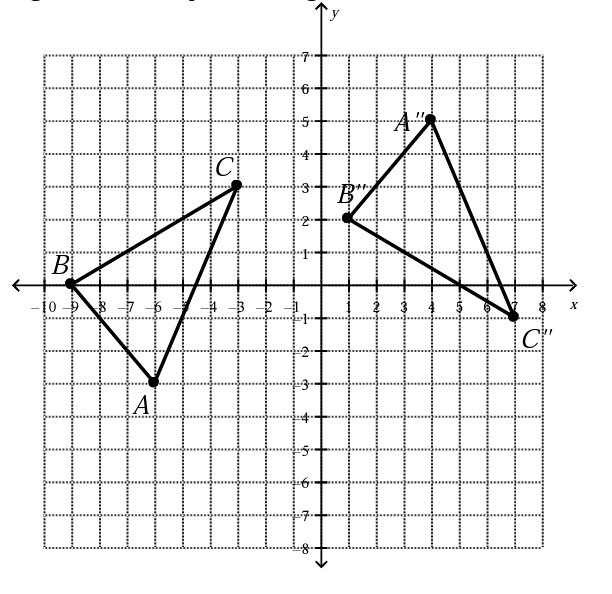
What is a Reflection across the x-axis and then translated 10 units right and 2 units up.