What tyoe of transformation involves moving a figure along a straight path without changing its position.
Translation
True or False: Two figures are congruent if one can be mapped onto the other using only translations, rotations, and refelections.
True
What happens to a figure when it is reflected over a line?
It is flipped across the line, creating a mirror image.
How many degrees are in full rotation?
360 degrees
Which of the following transformations preserves both the size and shape of a figure?
- A: Translation
- B: Rotation
- C: Reflection
- D: All of the above
D: All of the above
Explain why figure B is not the image of figure A after a 90* rotation around center P
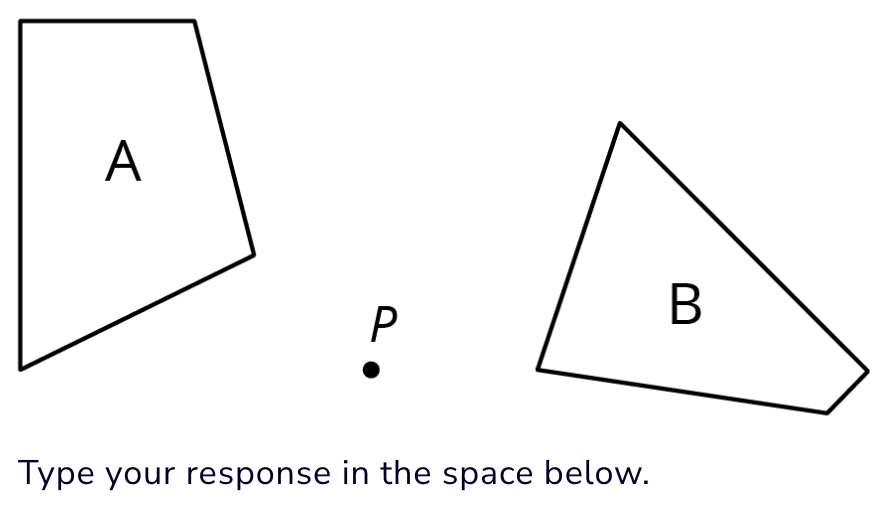
a. The shortest side of Figure A is shorter than the shortest side of Figure B. Since rotations do not change lengths, Figure B is not a rotation of Figure A.
b. The angles in Figure B do not match the corresponding angles in Figure A. Some of the angles in Figure A look like right angles while some corresponding angles in Figure B are definitely not right angles.
Can two rectangles be congruent if one has been rotated 90 degrees?
Yes, as long as the sides are equal in length.
What is the result of reflecting a shape twice over the same line?
The shape returns to its original position.
If a figure is rotated 90° clockwise, what transformation could undo the rotation?
A 90* counterclockwise rotation
Which property of a figure remains unchanged after a rigid transformaton?
- A: Area
- B: Shape
- C: Orientation
- D: Both A and B
D: Both A and B
Which sequence of transformations would NOT return a shape to its original position?
A: Translate 3 units up, then 3 units down.
B: Reflect over a line, then reflect over the same line again.
C: Translate 1 unit to the right, then 4 units to the left, then 3 units to the right.
D: Rotate 90° counterclockwise, then rotate 90° counterclockwise again.
D: Rotate 90° counterclockwise, then rotate 90° counterclockwise again.
Which of the following would prove that two quadrilaterals are congruent?
A: They have the same area.
B: They have the same side lengths and angles.
C: They have the same perimeter.
B: They have the same side lengths and angles.
True or False: A reflection changes the size of a shape.
False
True or False: A 180° rotation around the origin produces the same result as reflecting over both axes.
True
What is the name of the transformation that flips a figure over a line to create a mirror image?
Reflection
If a shape is rotated 180* about the origin, how does the position of the shape change?
The shape is upside down, but the size and shape remain the same.
How can you use rigid transformations to prove that two triangels are congruent?
By applying a combination of translations, rotations, or reflections to map one triangle onto the other.
Name a sequence of transformations that can take image P to image Q.
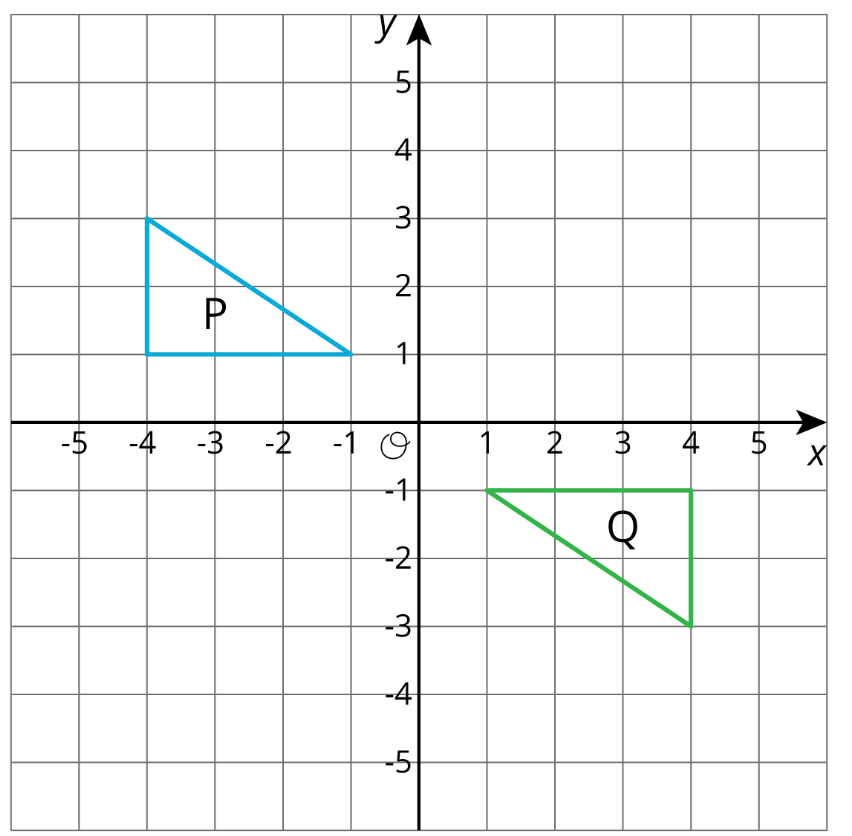
Teacher approved...
some examples: a reflection, and then a different reflection
a single rotation of 180* using (0,0) as the center
If a figure is rotated 270° counterclockwise, what is the equivalent clockwise rotation?
90* clockwise
Which of the following transformations changes the orientation of a figure but keeps it congruent to the original?
- A: Rotation
- B: Reflection
- C: Translation
- D: None of the above
B: Reflection
Point A is located at (-4,3) If you rotated A 180 degrees using (0,0) as your center, what are the coordinates of its image A'?
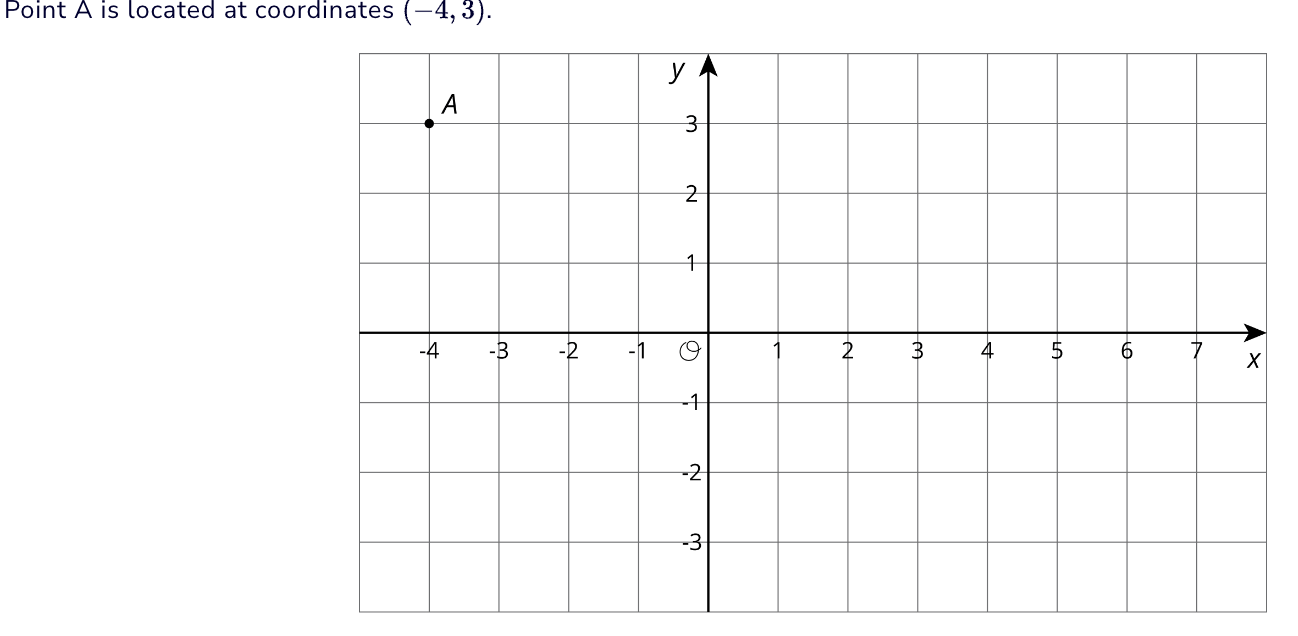
A' (4,-3)
Name all three requirements needed to perform a rotation.
Direction (clockwise, counterclockwise)
Angle (how far to rotate)
center of rotation (what are we rotating about?)
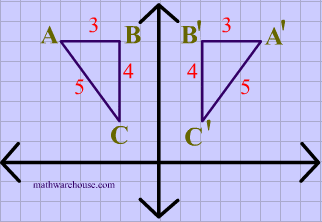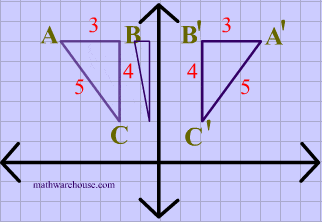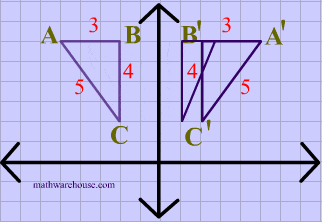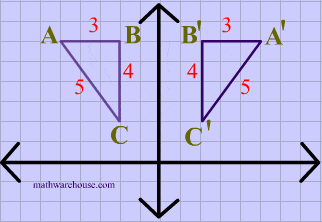 What transformation is this?
What transformation is this?
It's a reflection over the Y axis
How many kids does Mr. B have!
Mr. B has 2 kids
age 2.5yrs
age 4.5 years
Which rigid-transformaiton ALWAYS changes the position of a figure but keeps it congruent to the original?
A: Rotation
B: Reflection
C: Translation
D:A and B
D: Both A and B (Rotation changes orientation in some cases, but reflection always does).