Laws of Exponents
Expressions and Equations
Linear Functions
Systems of Equations
Pythagorean Theorem
100
Simplify completely.
42 * 46
48
100
Solve for x.
8x − 2 = −9 + 7x
x = -7
100
Define a function.
A relationship where each input has exactly one output.
100
What are the three methods for solving a system of equations?
Elimination, Substitution, and Graphing.
100
Draw a right triangle. Label the hypotenuse, the legs, and the right angle.
200
Simplify completely.
6x4/2x3
3x
200
Solve for n.
3n − 5 = −8(6 + 5n)
n = -1
200
Which functions are not linear? Select all that apply.
A. y=x+32
B. y= x/5
C. y=x2 +4
D. x+2y=3
E. y=27/x
C , E
200
Describe what a system of equation looks like graphically when the system has one solution, no solution, and infinitely many solutions.
One Solution: Lines intercept at one point which is the solution to the system.
No Solution: Lines are parallel (same slope) and never cross.
Infinite Solutions: Same line, and every point on the line is a solution.
200
Find the length of the missing side of a right triangle with sides a = 4 and b = 8
Approximately 8.9 OR 9
300
(5a2)(3a-5)
15/a3
300
Solve for a.
24a − 22 = −4(1 − 6a)
No Solution
300
Kizaiah and his friends decide to go bowling. The cost for the group is $15 for shoe rentals plus $4.00 per game.
Write an equation relating the total cost, C , of the outing to the number of games bowled, g.
C = 4g + 15
300
Write a system of equations to represent this situation.
Brenda's school is selling tickets to a spring musical. On the first day of ticket sales the school sold 3 senior citizen tickets and 9 child tickets for a total of $75. The school took in $67 on the second day by selling 8 senior citizen tickets and 5 child tickets.
3s + 9c = 75
8s + 5c = 67
300
Find the length of the missing side of a right triangle with a leg of length 3.9 and a hypotenuse of length 11.
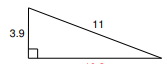
Approximately 10.3 OR 10
400
Simplify completely.
(2x2yz3)(3x-3y3)
6y4z3/x
400
Find one value for P and one value for Q so that there are infinite values of x that make the equation true.
2(6x +0.5) = Px + Q.
P = 12 , Q = 1
400
The Ace Telephone Co. charges a flat monthly fee of $22.00 for a telephone line and $0.20 per minute for long distance calls.
How many calls could you make if your phone budget is $30?
40 calls
400
The length of a rectangle is equal to triple the width. Which system of equations can be used to find the dimensions of the rectangle if the perimeter is 86 centimeters?
l= 3w
2l + 2w = 86
400
Would a triangle with the side lengths 15, 17, 8 represent a right triangle? EXPLAIN!
Yes, because 82+152=172
500
Simplify completely.
(2-1)(3-2)
1/18
500
You work as a babysitter on the weekends to save up money for the summer. Your total charge C is $5 to babysit plus $10 for each hour. What equation can be used to find the total cost for when h hours are used?
C = 10 h + 5
500
A machine salesperson earns a base salary plus a commission for every machine he sells. The linear model representing the salesperson’s total income is y = $300x + $40,000.
Interpret what each part of this equation represents in the context of this problem.
The y-intercept is $40,000; the salesperson earns a $40,000 salary in a year and that amount does not depend on x. The slope is $300 because the salesperson’s income increases by $300 for each machine he sells.
500
Some students want to order shirts with their school logo. One company charges $9.65 per shirt plus a setup fee of $43. Another company charges $8.40 per shirt plus a $58 fee. For what number of shirts would the cost be the same?
12 shirts
500
A palm tree casts a 14 foot shadow. The end of the shadow is 22 feet from the top of the tree. How tall is the tree?
Approximately 17 feet.