The incenter is equidistant from the ______
Sides of a triangle
Which of the following is not a triangle congruence theorem: SSS, AAA, ASA, SAS, HL
AAA
The segments that create the incenter?
The angle bisectors
The segments that create the circumcenter?
Perpendicular Bisectors
Find FQ if T is the centroid 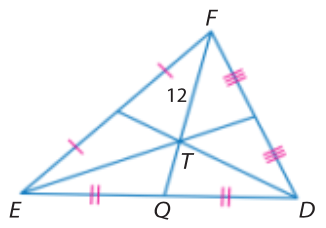
18
What does the midsegment of a triangle connect?
Midpoints of sides.
What do we call these sets of numbers? (among others)
3,4,5
5,12,13
8,15,17
7,24,25
Pythagorean triples
The altitudes intersect at the ________
Orthocenter
A statement formed by both negating and exchanging the hypothesis and conclusion.
Contrapositive
Find XZ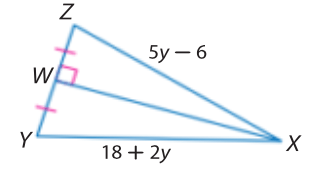
34
The balance point of a triangle
The centroid
If the midsegment of a triangle is 3x+3 and its opposite side is 4x+7, what is the value of x?
1/2
What do we call this?
If B is between A and C then AB + BC = AC.
Segment addition postulate
If Z is the circumcenter find RZ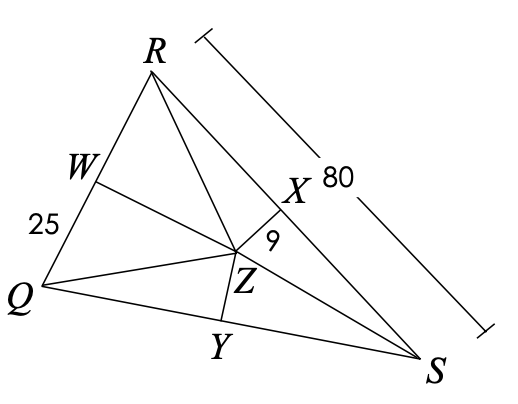
41
Find EG if G is the incenter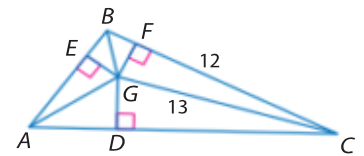
5
What is true about the 6 triangles created by drawing in the medians on a triangle
Equal area
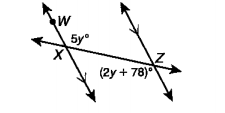
What is the measure of angle WXZ?
130˚