Congruence
Proofs 1
Proofs 2
Transformations
Definition
100
Name the method used to prove the triangles are congruent.
SAS
100
Name the five ways to prove triangles are congruent.
SSS, SAS, AAS, ASA, SSA (with the opposite side of given angle is longer)
100
Name what CPCTC stands for
Corresponding Parts of Congruent Triangles are Congruent.
100
When geometric shape is flipped across a line and what is the line called?
reflection and line of reflection
100
Something that cuts a geometric object into two equal parts
bisector
200
If so, name the method.
Yes and ASA
200
Name the reason that segment KA is congruence to segment KA.
The segments are congruent to themselves.
200
Name the important feature to remember when naming corresponding angles?
Write then in corresponding order
200
When a geometric shape is slided from one place to another
translation
200
Two lines that meet at a right angle
perpendicular lines
300
no (should be SSS)
300
Name the reason used to prove
angle
ACB is congruent to
angle
ECD.
The vertical angle theorem.
300
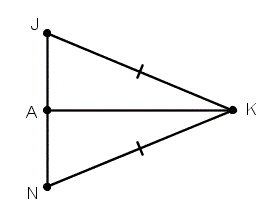
AK is the angle bisector of angle JKN. Name the two congruent angles in corresponding order.
angleJKA congangleNKA
300
When a geometric shape is moved in a circular motion
rotation
300
A line that intersects two parallel lines
transversal
400
triangle ABC congtriangleJKI
400
Name what must be written in the given statement to use the reason alternate interior angles theorem to prove two angles are congruent.
parallel lines
400
Something we already proved and accept
Theorem
400
When a geometric figure is increased or decreased in size
dilation
400
Definition of similar figures
all corresponding angles are congruent and all corresponding sides are proportional.
500
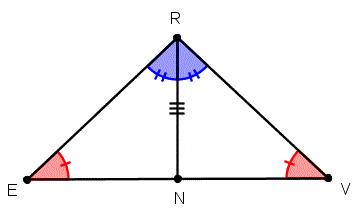
Using the markings on the triangles name the method used to prove the triangles are congruent and write a congruence statement.
AAS
triangleENR congtriangleVNR
500
Name the two methods that don't work to prove triangles are congruent.
AAA and SSA (with opposite side of given angle is shorter)
500
What theorem does this statement show?
In triangleFGH,
if bar(FG) cong bar(HG),
then angleH cong angleF.
Isosceles Triangle Theorem
500
This is preserved in all rigid transformations (except dilation)
size
500
Rectangles and isosceles trapezoids have this feature in common
congruent diagonals