Proof Strategy
Triangle Properties
Congruence Theorems
Proof Steps
Miscellaneous
100
What are the main statements we say at the beginning of a proof and at the end of a proof?
What are: the given (at the start)
The prove statement (at the end)
100
How do we know that <AEC=<DEB below?
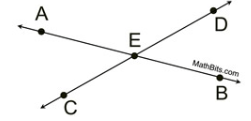
What are vertical angles?
100
Side Side Side
What is SSS
100
What is the "Reason" for Statement #1 below?
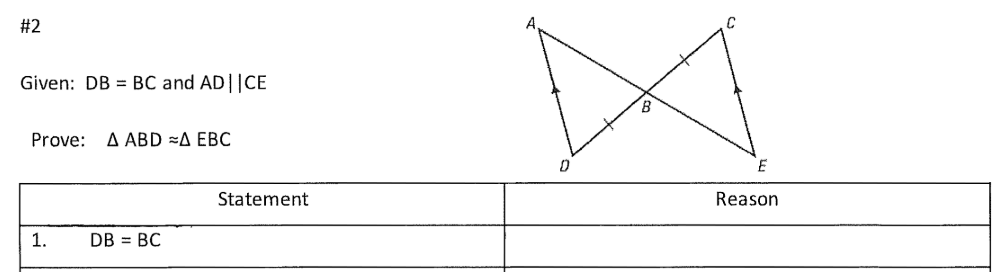
What is "given"?
100
If the vertex angle of an isosceles triangle is 30 degrees, what is the measure of the other two angles?
75 degrees
200
What reason can you give to show the same figure is congruent to itself?
Reflexive Property
200
How do we know that CA=CA below?
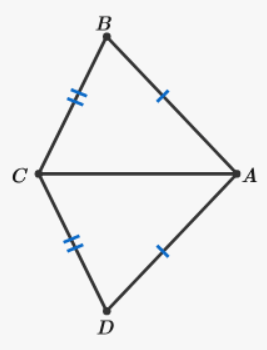
Line segments are congruent to themselves
200
If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then these two triangles are congruent.
What is SAS
200
What is the reason for statement #3 below?
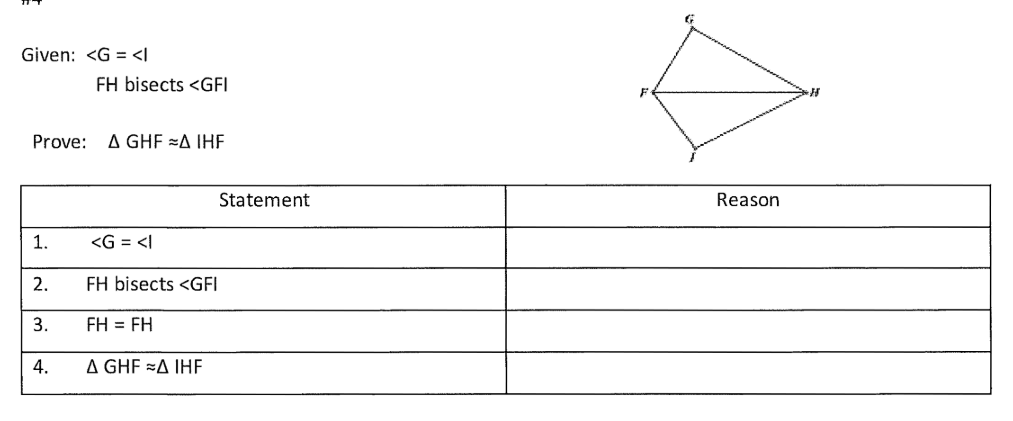
Reflexive Property
200
Name the triangle congruence theorems we learned.
What are SSS, SAS, AAS, ASA, HL
300
What do we call a statement that looks like below?
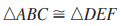
(Triangle) Congruence Statement
300
Name the 4 angles that point "E" the vertex of?
1) <AEC (or <CEA)
2) <DEB (or <BED)
3) <AED (or <DEA)
4) <CEB (or <BEC>
NOTE:
300
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then these two triangles are congruent.
What is ASA
300
What is the reason for statement #3 below?
Definition of Vertical Angles
300
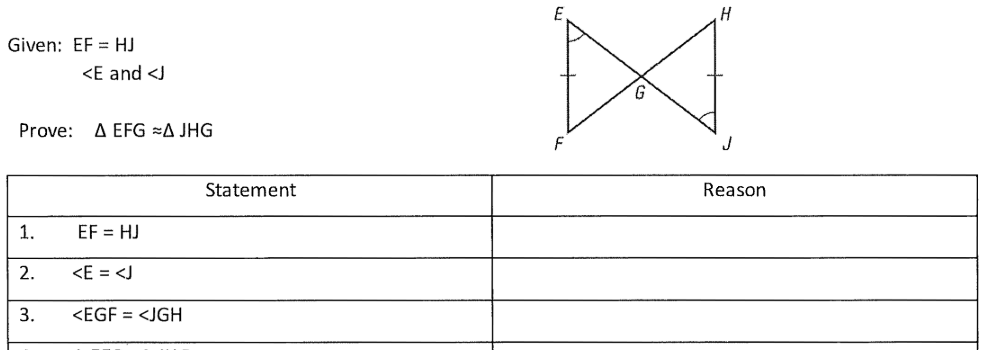
Given the congruence statement below, what is congruent to CB?
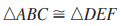
What is FE?
400
Identify the corresponding part to angle C
Angle R
400
In the triangle below, if "D" is the midpoint of AC, what is AD congruent to?
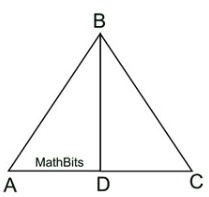
What is DC?
400
If two angles and the non-included side one triangle are congruent to two angles and the non-included angle of another triangle, then these two triangles are congruent.
What is AAS
400
What is the reason for statement #2 below?
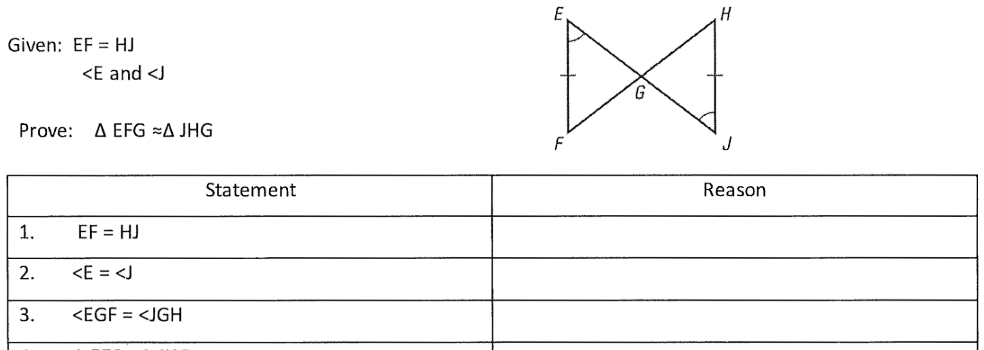
Definition of Alternate interior angles
400
What congruence theorem can be used to prove the triangles below are congruent?
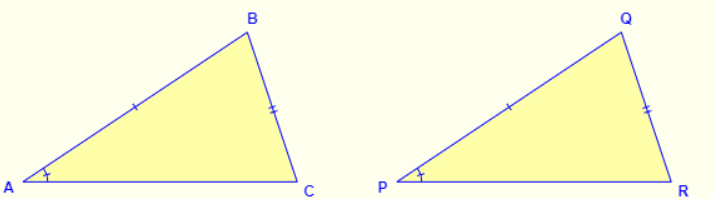
Not congruent.
SSA is not a congruence theorem.
500
You've completed enough of the proof to show that the triangles below are congruent:
What rule(s) do you need to show that B is a midpoint of AE?
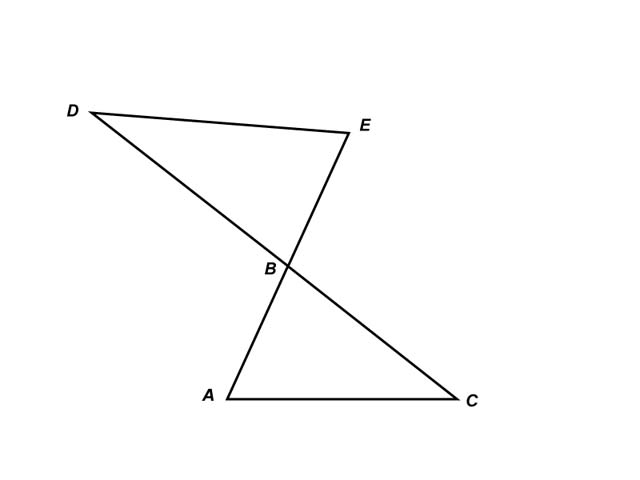
CPCTC
and
Definition of midpoint
500
IF DB bisects <B, what angle is <DBC congruent to?
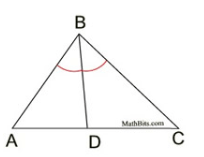
<DBA or <ABD
500
If you were given DE // AC in the triangles below, what additional piece of information would you need to prove the triangles congruent?
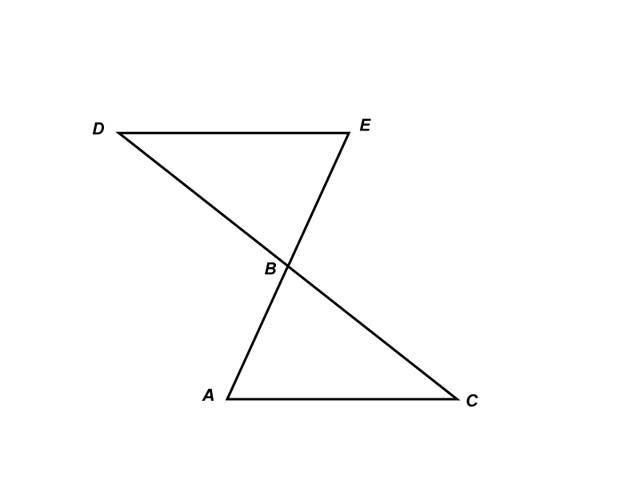
one pair of side lengths.
Example: DE = AC
500
In the triangles below, AD // CE. Prove the triangles are congruent.
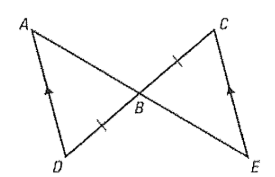
Note; <A = <E *AND* <D = <C, by Alternate interior angles.
Should use ASA or AAS, depending on steps.
500
Name the 3 congruence theorems that could be used to prove the triangles below are congruent.
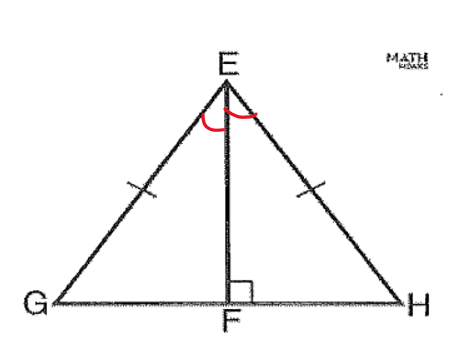
What are SAS, AAS, HL?