CPCTC
SSS and SAS theorem
ASA and AAS theorem
HL theorem
Equilateral triangles
100
What does CPCTC stand for?
What is corresponding parts of congruent triangles are congruent
100
What does SAS stand for?
What is side-angle-side
100
What does ASA stand for?
What is angle-side-angle
100
7State how these triangles are congruent
HL theorem
100
Find the value of X
X=11
200
When do you use CPCTC in a proof?
What is always in the end of a proof
200
What postulate would prove 2 triangles are congruent using all 3 sides of the triangles?
What is SSS
200
State how the triangles are congruent
AAS
200
are these two congruent.
Following the HL theorem, in △ABC and △PQR: BC = QR (congruent hypotenuse)
Thus, y = 13
AC = PQ (congruent legs)
Thus, x = 5.
Therefore, x = 13, y = 5
200
Find the value of X
X=-9
300
What must be done first when dealing with CPCTC
what is triangles proven congruent
300
What postulate proves 2 triangles using 2 sides and an angle?
What is SAS
300
state how these triangles are congruent
ASA
300
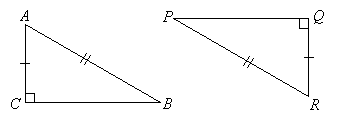Are these two congruent?
In the following right triangles ΔABC and ΔPQR , if AB = PR, AC = QR then ΔABC ≡ ΔRPQ .
300
Find the value of X
X=-1
400
True or false CPCTC can be used for just sides?
what is false
400
Are the triangles similar? If so, what theorem proves it?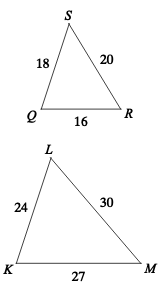
SSS similarity
400
The method used is: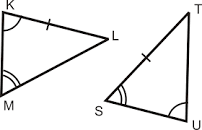 
What is AAS
400
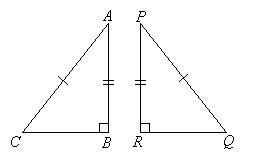Are these Triangles congruent?
ΔABC and ΔPQR are right triangles
AC = PQ (hypotenuse)
AB = PR (leg) So, triangle ABC and triangle PQR are congruent by the Hypotenuse Leg Theorem.
400
Find the value of X
X=10
500
True or False CPCTC can be used at any point during the proof?
What is False
500
Are the triangles similar? If so, what theorem proves it?
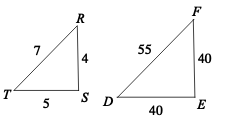
Not similar
500
ASA is a congruence ___________.
What is postulate?
500
prove that △PSR ≅ △PQR.
It is given that △PSR and △PQR are right-angled triangles.
PS = QR (equal legs, given)
PR = PR (equal and common hypotenuse)
Hence, △PSR ≅ △PQR (by HL rule)
500
Find the value of X
X=-7