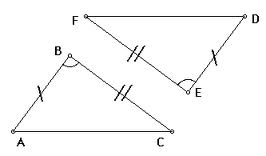
 Are these 2 triangles congruent?
Are these 2 triangles congruent?
Yes, they are congruent by SAS
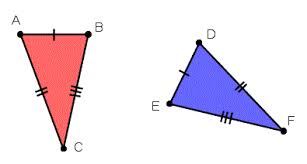
Given:
C is the midpoint of BD and AE
Definition of a midpoint means that AE = ?
BD
Are these triangles congruent? 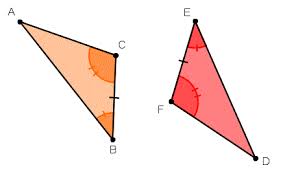
Yes, they are congruent by ASA
If angle and A and angle B are a linear pair then the angles are
Supplementary
total 180 degrees
 Are these two triangle congruent?
Are these two triangle congruent?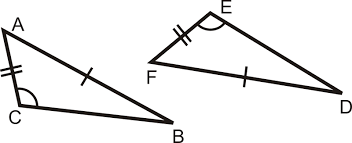 Is this proved by SSS?
Is this proved by SSS?90
Angles that are complementary total ____ degrees
90
ninety
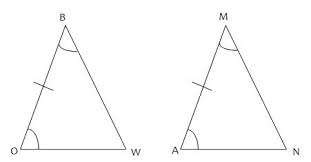
 Which postulate proves that these two triangles congruent?
Which postulate proves that these two triangles congruent?Are these triangles congruent?
Yes, the triangles are congruent by SSS
BC = ?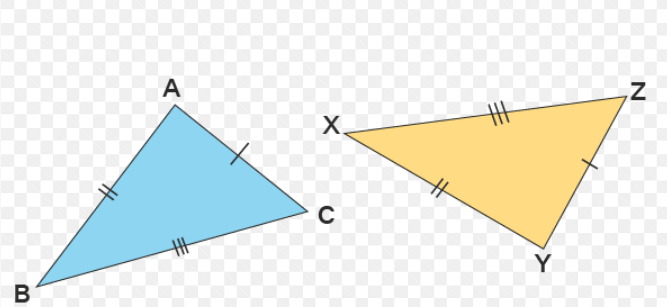
XY or YX
The sum of the interior angles of a pentagon
540 degrees
180
Are these triangles congruent by SSS?
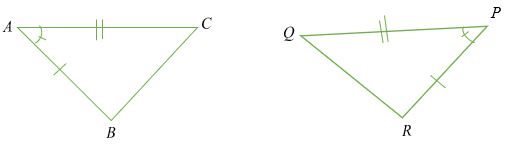
No, they are congruent by SAS
A, B and C are collinear
Given B is the midpoint between A and C.
So BC =
Segment AB
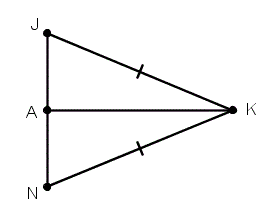
Are these triangles congruent by ASA?

Yes, they are.
If you have a quadrilateral, the sum of the interior angles is
How many pieces of evidence does one need to prove two triangles are congruent?
3 Three
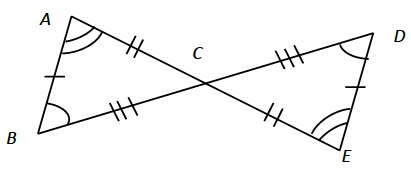
Are these triangles congruent? If so, write a congruency statement.
What is
triangleABCcongtriangleEDC
Vertical angles are ___________
congruent or equal