Inverse Trig
Trig Ratios
Distance!
Pythagorean Theorem
Application Problems
100
Find the missing angle measure, denoted with the question mark.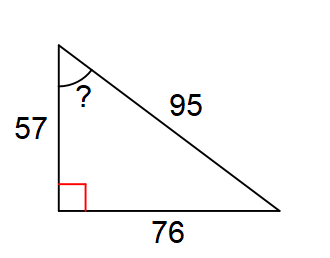
53 degrees
100
What is the tangent ratio given that theta is angle A?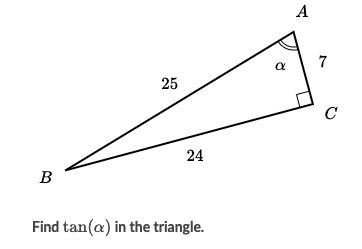
24/7
100
Find the distance between (-3, 6) and (9, -5).
To the nearest 10th!
16.3 units.
100
The missing side of the right triangle when a=6 and c=10.
What is b=8?
100
The sun is 62 degrees above the horizon. A tree casts a shadow that is 12 feet long. How tall is the tree?
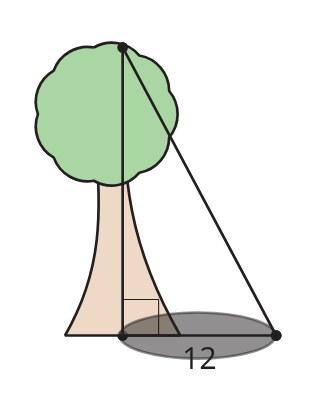
26.2
200
Solve for the measure of angle B.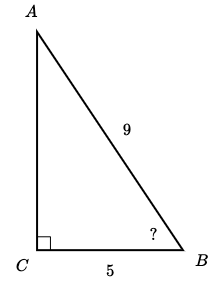
angle B = 56.25 degrees
200
What is the value of x?
x=43.8
200
8. Write an example of a point that would fall on the horizontal line segment with one endpoint (5, 13)
One such point could be (7,13) - y coordinate has to be 13
200
The missing side of a right triangle when b=9 and c=15.
What is a=12?
200
A man flies a kite and lets out 100 feet of string. The angle of elevation of the string is 52 degrees . How high off the ground is the kite?
78.8 ft
300
You are given a right triangle with a known angle of 33.7 degrees. What are the degrees of the other two angles?
What is 90 and 56.3 degrees?
300
What trig ratio do you need to use to solve for BC? What is the length of BC?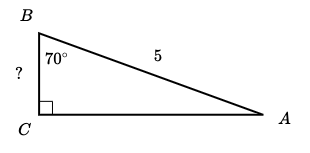
Cosine
BC = 1.71
300
Mr. Franklin needs to draw a perfect circle. The endpoints of one of the diameters needs to fall on (7, 1) and (−1, −1). Where should he locate the center of the circle?
The center of the circle is located at (3,0)
300
Do the side length 34, 25.5 & 44.7 create a right triangle?
What is NO?
300
The sun shines on a flagpole, causing a shadow to be cast on the ground. The distance from the base of the pole to the tip of the shadow is 49 feet. At that time of day, the sun’s rays make an angle of 38 degrees with the ground. How tall is the flagpole?
38.3 ft
400
The angle of inclination, from a point on the ground 30 feet away from the base of a water tower, to the top of the water tower, is 60°. Find the height of the water tower to the nearest foot.
52 feet tall.
400
An angle in a Right triangle is 56 degrees and the adjacent side is 16 degrees, what is the hypotenuse to the nearest 10th.
What is 28.6?
400
Fred is at Bojangles which is 2 miles west and 4 miles north of the school. Barney is at Pelicans which is 4 miles east and six miles south of the school. How far apart are Fred and Barney? (to the nearest 10th
Fred and Barney are approximately 11.67 miles apart.
400
Name two 'special right triangles'
What is 3,4,5 and 5,12,13
400
A plane leaves the ground with an elevation angle of 6 degrees. The plane travels 10 miles horizontally. How high is the plane at the time?
1.1 Miles
500
In order to determine the height of a California redwood tree, two sightings from the ground, one 200 feet directly behind the other, are made. If the angles of inclination were 45° and 30°, respectively, how tall is the tree to the nearest foot.
The tree is approximately 273 feet tall.
Tan(45)= h/ x and tan(30) = h/x+200
500
A right triangle with an angle of 55 degrees has a hypotenuse of 20 miles, what is the opposite side length to the nearest 10th. Be precise.
What is 16.4 ?
500
A triangle has vertices at (1, 3), (2, −3), and (−1, −1). What is the approximate perimeter of the triangle (to the nearest hundreth)?
The approximate perimeter of the triangle is 14.16 units.
500
The missing side of a triangle when a=14 and c=48.
Round to a hundredth if necessary
What is b=45.91?
500
In order to determine the height of a radio tower, two sightings from the ground, one 150 feet directly behind the other, are made. If the angles of elevation were 40° and 25°, respectively, how tall is the tower to the nearest foot?
The height of the radio tower (h) is approximately 157 feet.
tan(40∘)=h/x
tan(25∘)=h/x150h