Convert from degrees to radians
44o
(11pi)/45
How does C affect the function
y=Csin(x)
Makes the amplitude C
What are the three pairs of trig functions that when multiplied equal 1
cos and sec
sin and csc
tan and cot
What is the difference between the capital and lowercase letters in the law of sines and law of cosines?
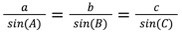
Uppercase= angles
Lowercase= sides
Graph -2+5i on the complex plane
left 2 up 5
Convert from radians to degrees
(8pi)/9
160o
How does C affect the function
y=sin(Cx)
Makes the period C times faster
Prove the trig equality
cos(x)sec(x)-sin^2(x)=cos^2(x)
1-sin^2(x)=cos^2(x)
cos^2(x)=cos^2(x)
When is it necessary to use the law of cosines instead of law of sines?
When you don't have an angle and its opposite side
Graph 5-2i on the complex plane
Right 5 down 2
Find the six trig functions
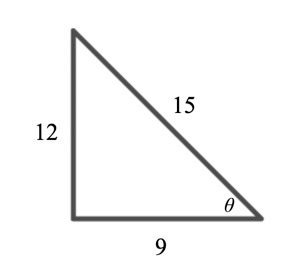
sin(x)=12/15, csc(x)=15/12
cos(x)=9/15, sec(x)=15/9
tan(x)=12/9, cot(x)=9/12
Create a graph of cos(x) and use to graph sec(x)
make sure zeros become asymptotes
Prove the trig equality
cos(cos+secsin^2)=1
cos^2+sin^2=1
1=1
If u=<-2,4>, v=<3,2> and w=<-1,5> Find
(u*v)w
<-2,10>
What is the shortcut when multiplying a number by its complex conjugate?
a2+b2
Find sin, cos and tan for the following (not on the unit circle) given a point (x,y) and a radius
r=13 (5,12)
sin(x)=12/13
cos(x)=5/13
tan(x)=12/5
Using your Unit Circle find
arccos(-1/2)
(2pi)/3 and (4pi)/3
Use the sum and difference formulas to solve
cos(15^o)
cos(45-30)
(sqrt6+sqrt2)/4
Find the slope, magnitude and unit vector of the vector with initial point (-3,2) and terminal point (1,10).
vector is <4,8>
slope is 2
"magnitude is " sqrt80
"Unit vector is "<4/sqrt80,8/sqrt80>
"Simplify "(3+i)(3-i)
Find sin, cos and tan for the following (not on the unit circle) given a point (x,y) and a radius
r=10 (-8,6)
sin(x)=6/10
cos(x)=-8/10
tan(x)=6/-8
A water tower that is 48 feet high casts a shadow along the ground that is 60 feet long. What is the angle of elevation, A, of the sun?
~~38.66^o
Use the sum and difference formulas to solve
sin(195^o)
sin(225-30)
(-sqrt6+sqrt2)/4
Find the dot product of u=<3,-4>, v=<5,1> Are they orthogonal?
11, so no because not 0
"Simplify "(1+sqrt5i)(1-sqrt5i)
6