Right Triangle Trig
Special Triangles and Unit Circle
Trigonometric Function Graphs/Law of sines and cosines
Trig Identities and Proving Equivalence
100
Do these three sides make a right triangle?
a = 3.3 b = 8.7 and c = 9.3
Yes!
100
Find f and g.
f = 10 and g = 10sqrt3
100
Fill in the blanks:
The sine graph crosses the y-axis at ___________.
The cosine graph crosses the y-axis at ___________.
1. the origin/the point (0,0).
2. The point (0, 1)
100
Fill in the blanks.
Tanx = _____ over _____
_______ + cos^2x = ______
sin/cos
sin^2x/1
200
Which trigonometric function should you use to solve for x?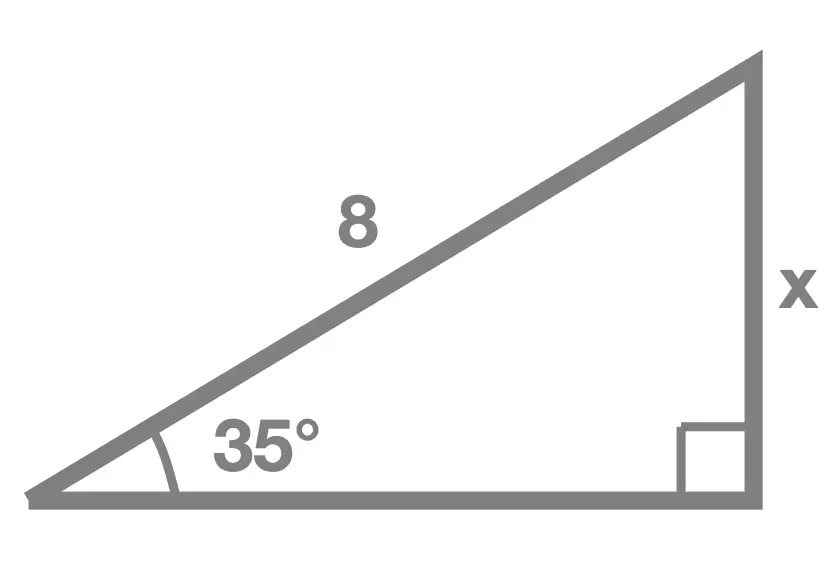
sine
200
Convert 2500 into radians.
25pi/18
200
What transformations are represented by the equation below? y = 5cos(2(x+pi/2))-3
5- vertical stretch (amplitude)
2- horizontal compression (period is pi)
pi/2- horizontal shift pi/2 to the left
-3- vertical shift down 3
200
Use a reciprocal trig function in order to solve BC. Round to the nearest tenth.
13.2 units
300
Calculate angle A in degrees. Round to the nearest tenth.
36.90
300
Plot and label the point on a unit circle for the radians 4pi/3.
(-1/2, -sqrt3/2)
300
Write an equation for the tangent function with the following transformations: a horizontal shift of pi to the right, a vertical shift down 4 and a vertical stretch of 3.
y = 3tan(x - pi) - 4
300
Prove equivalence: sin(x)cos(x) = sin(x)/sec(x)
sin(x)cos(x) = sin(x)/sec(x)
sin(x)*cos(x) = sin(x)/[1/cos(x)]
sin(x)cos(x) = sin(x)cos(x)
400
Round to the nearest tenth.
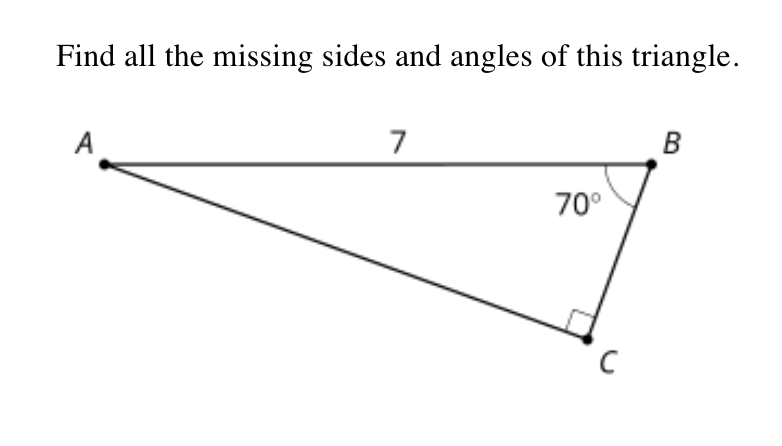
Angle A is 200, side a is 2.4 and side b is 6.6
400
What is arccos(0)? You should include your TWO answers in radian form.
pi/2 and 3pi/2
400
Find the missing side:
a=9.3 C = 1120 b = 5
12
400
Prove csc(x)cos(x)tan(x) = 1
[1/sin(x)]cos(x)*[sin(x)/cos(x)] = 1
sin(x)*cos(x)/[sin(x)*cos(x)] = 1
1 = 1
500
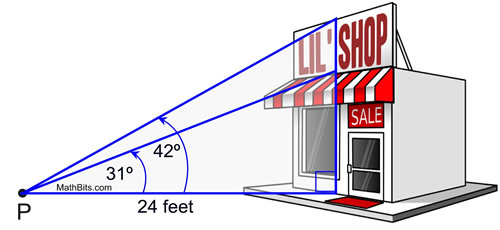Simon bought a new shop and wants to order a new sign for the roof of the building. From point P, he finds the angle of elevation of the roof, from ground level, to be 31º and the angle of elevation of the top of the sign to be 42º. If point P is 24 feet from the building, how tall is the sign to the nearest tenth of a foot?
7.2 feet
500
Describe the patterns for each of the 4 components of the unit circle.
Angles go 30/15/15/30
Radians go 6/4/3/3/4/6 and Q1 is pi, Q2 is denominator -1, Q3 is denominator +1, Q4 is denominator*2 and -1.
Coordinates are all square roots over 2, they are + or - based on which quadrant they are in. The numerators are all 3, 2, 1 and then 1, 2, 3.
500
Find all three missing angles. Round to the nearest tenth.
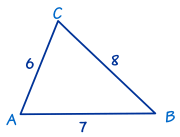Daily Double!
A = 75.50
B = 46.60
C = 57.90
500
cot(x)sin(x)cos(x) + sin2(x) = cos(x)/[cot(x)sin(x)]
cot(x)sin(x)cos(x) + sin2(x) = cos(x)/[cot(x)sin(x)]
cos(x)/sin(x) * sin(x)cos(x) + sin2(x) = cos(x)/ cos(x)/sin(x) * sin(x)
cos(x)*cos(x) + sin2(x) = cos(x)/cos(x)
cos2(x) + sin2(x) = 1