What is the initial amount and growth factor for the function f(x)=2(3)x
initial amount=2
growth factor= 3
How do I know if an exponential function is exponential growth or decay from an equation?
Growth has a b value or growth factor greater than 1 and decay has a b value or decay factor less than 1
Convert to exponential form: cube root of a
a^(1/3)
x^0
1
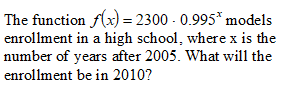
2243
What is a1 and r of the following sequence?
2, 6, 18, 54, ...
a1=2 and r=3
Becky invested $19,800 in a CD that pays an annual interest rate of 5.3%. The CD is set to compound daily. How much is in Becky’s account after 9 years? (Note: Ignore the extra day from leap year.)
$31,901.32
Does the following function represent growth or decay? What is the rate?
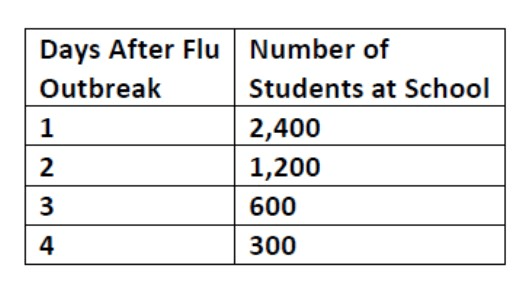
Decay, rate of 50%
Convert to radical form: x^(10/7)
Seventh root of x^10
(a^3b^-2c^8)^-2
b^4 / a^6 c^16
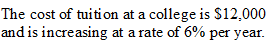
What will be the cost in 17 years?
$32,313.27
Write the explicit formula for this geometric sequence.
-1,-3, -9, -27, ...
-1(3)^(n-1)
Find the rate given the coordinates; (0, -2) (3,4)
2
f(x)=2(1.13)x
Does this function represent exponential growth or decay? What is the growth/decay RATE?
Exponential Growth
Rate: 0.13 or 13%
Simplify fully!
t^(2/5) x t^(1/10)
square root of t
(x^5 y^4 / x^-2 y^3)^-3
1/ x^21 y^3
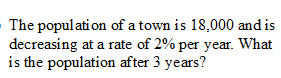
16,941 people
Find the 7th term of the geometric sequence:
55, 165, 495, 1485, ...
a7=40095
a) What is the y-intercept?
b) Is it Growth or Decay?
c) What is the equation of the graph?
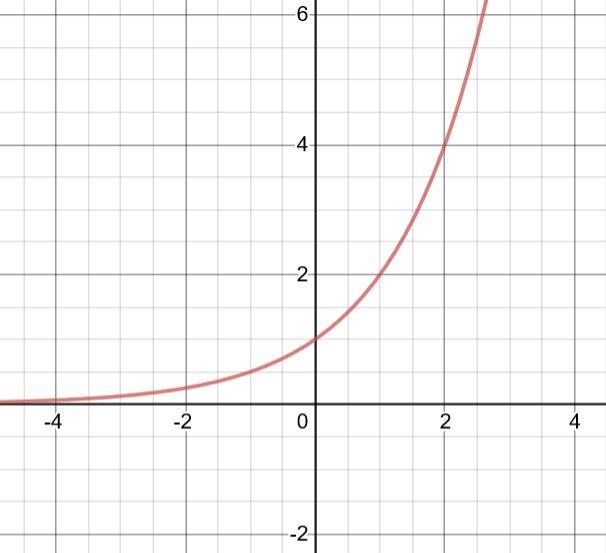
a) (0,1)
b) growth
c)y=1(2^x)
f(x)=5(0.97)x
Does this function represent exponential growth or decay? What is the growth/decay RATE
Exponential Decay
Rate: 0.03 or 3%
Simplify fully:
m^(7/8) / m^(2/3)
24th root of m to the 5th
(5/2)^-4
16/625
A radioactive isotope with a 6-hour half-life starts with 100 mg. How much of the isotope is left after 3 days?
y=100(0.5)^72/6=0.02 mg
Find the 15th term of the geometric sequence.
100, 50, 25, 12.5, ...
a15=0.006
Write the equation to the following table:
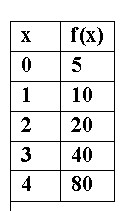
y= 5(2)x
Dr. Higgins purchased a car for 86,400 and every year it decays by 12%. What can he expect the value of his car to be after 24 months?
f(x)=86400(.88)^2=$66,908.16
(xy^2)^1/3 / y
cube root of x over the cube root of y
(2xy^-5 / 10x^3 y^8) ^-2
25x^4 y^26
If you have a balance of $580 after 5 years in an account earning a 3% yearly compound interest rate, how much was initially deposited?
$500.31
Find the formula for the following geometric sequence if a1=2 and a4=54. Use algebra to prove your formula.
an=2 x 3^n-1