Exponent Rules
Functions
Average Rate of Change
Translations
Systems of Equations
100
Fully simplify:
(2x^2y^4)^5
32x^10y^20
100
The graph of y=f(x) is graphed below. What is the end behavior of f(x)?
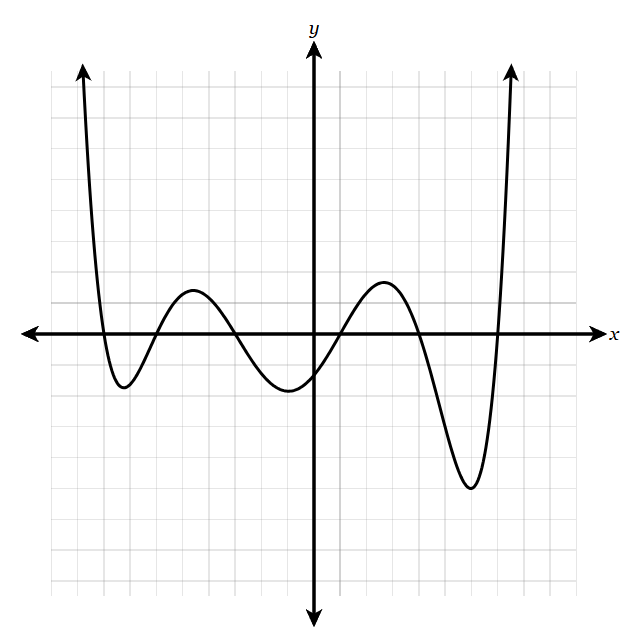
As x->\infty, y->\infty
As x->-\infty, y->\infty
100
Using the table, find the average rate of change on [12, 30].
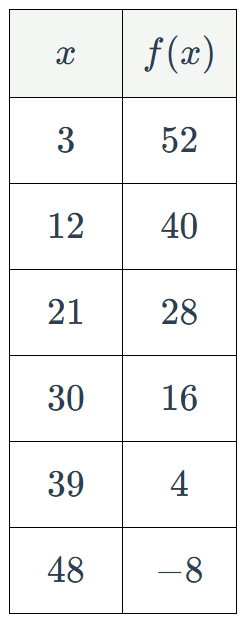
-4/3
100
What transformation of y=sqrtx has been applied?
y=sqrtx-5
Shift down 5 units
100
Solve the following system of equations graphically on the set of axes below.
y=-x+7
y=3/2x-3
(4, 3)
200
Fully simplify:
(-2x^2y^5)^3
-8x^6y^15
200
The graph of y=f(x) is graphed below. What is the end behavior of f(x)?
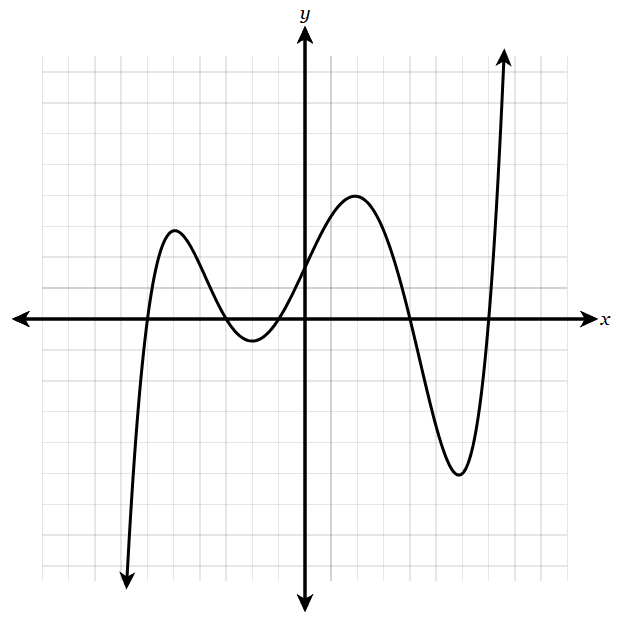
As x->\infty, y->\infty
As x->-\infty, y->-\infty
200
Find the average rate on [-6, 4] using the graph.
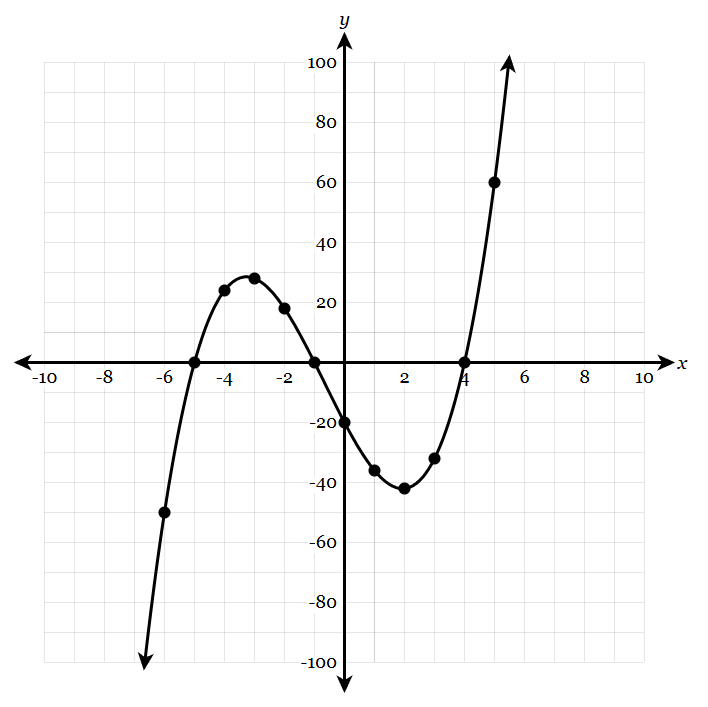
5
200
Given the parent function f(x)=x^3, the function g(x)=(x-1)^3-2 is the result of a shift of f(x) ...
1 unit right and 2 units down
200
Solve the following system of equations graphically on the set of axes below.
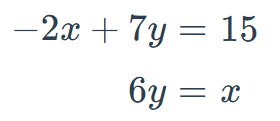
(-18, -3)
300
Fully simplify using only positive exponents.
(4xy^8)/(x^8y^7)
(4y)/x^7
300
State the equation of the vertical asymptote:
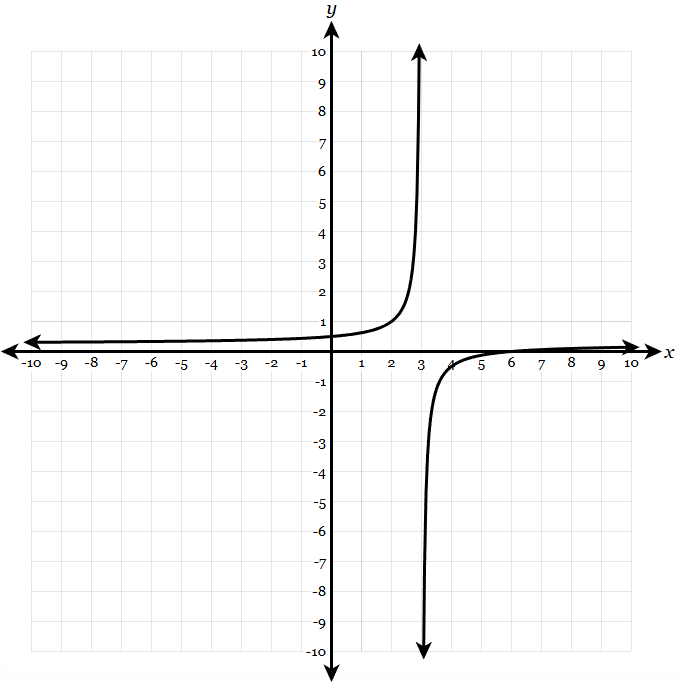
x = 3
300
Given the function f(x)=-x^2+5x+14 , determine the average rate of change of the function over the interval [-2, 9].
-2
300
Write the equation of a function g(x) which would shift the graph of f(x)=-|x| right 3 units.
g(x)=-|x-3|
300
Solve the system by substitution.
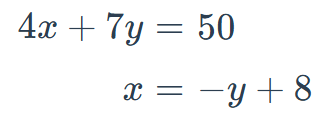
(2, 6)
400
Fully simplify using only positive exponents.
(10x^2y^3)/(4x^5y^2)
(5y)/(2x^3)
400
State the domain and range of the function:
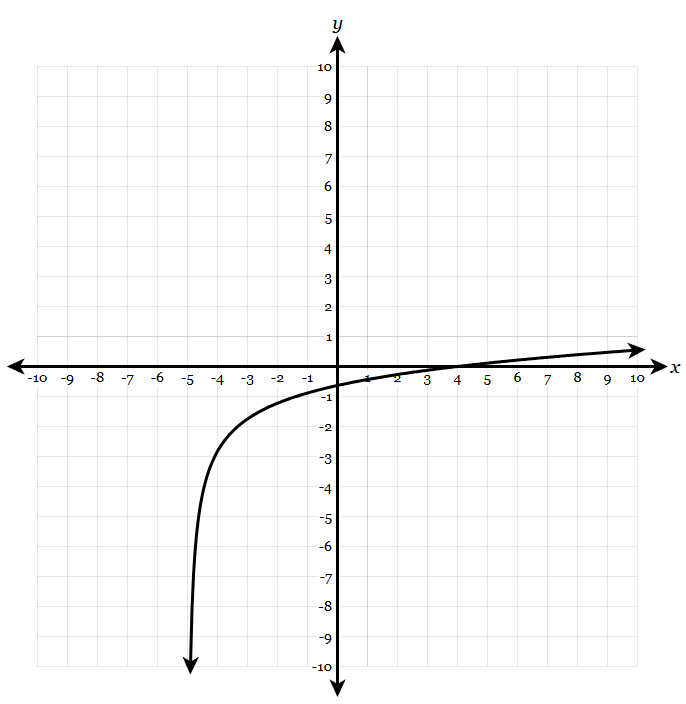
D: (-5, infty)
R: (-infty, infty)
400
Compare f(x) and g(x). Which function has the smallest average rate of change for -1<=x<=4 ?
g(x)=x^2+3x+20
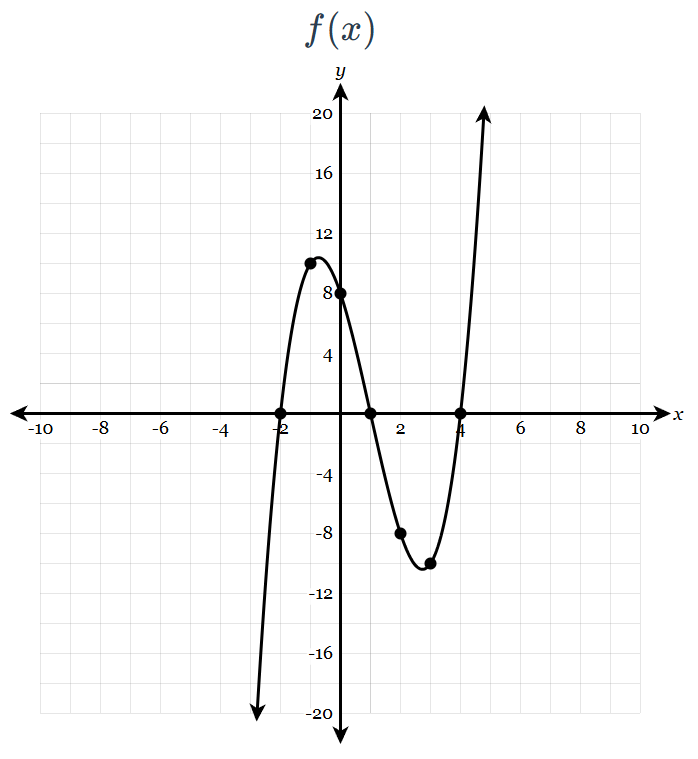
f(x)
400
Write the equation of g(x) which would shift the graph of f(x)=1/x left 2 units and up 4 units
g(x) =1/(x+2) +4
400
Find the solution to the system of equations.
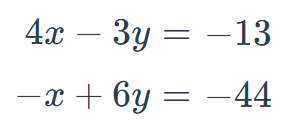
(-10, -9)
500
Express the following fraction in simplest form, only using positive exponents.
(10d^3)/(-2d^-5)^3
-(5d^19)/4
500
State the domain and range of the function:
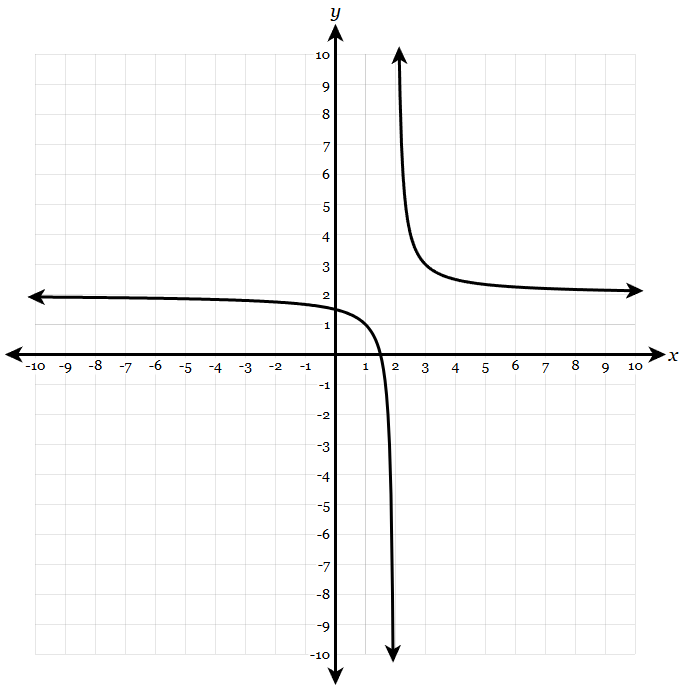
D: (-\infty, 2)cup(2, \infty)
R: (-\infty, 2)cup(2, \infty)
500
A fruit fly population can be modeled by the equation P=10(1.27)^t , where P represents the number of fruit flies after t days. What is the average rate of change of the population, rounded to the nearest hundredth, over the interval [0, 10.5]? Interpret your answer in the context of the question.
10.76 fruit flies/day
The fruit fly population is increasing at a rate of 10.76 fruit flies per day.
500
Write the equation of a function g(x) which would shift the graph of f(x)=3^x left 6 units and down 2 units.
g(x)=3^(x+6)-2
500
Find the solution of the system of equations.
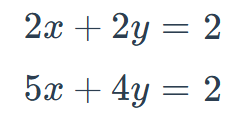
(-2, 3)