Freebie: Draw an emoji based on how you're feeling for the test
:)
What are the 3 transformations we have discussed in unit 1?
translation, rotation, reflection
What is a line of symmetry?
The vertical line that divides the graph or figure into two congruent halves, sometimes called axis of symmetry.
Two geometric figures are defined to be congruent if there is a sequence of rigid motions that carries one onto the other.
Congruency of angles and side lengths have the same measure.
In the equation of a line y=mx+b,
which letter represents slope?
m
What is a translation?
A transformation that locates points at the same distance and direction along lines that are parallel to each other
Describe the transformation
reflection over y=x
If a figure has rotational symmetry, it means...
the figure can be carried onto itself by a rotation of a certain degree.
How can I prove with rotations that angle C is congruent to angle A?
rotate 180 degrees
Perpendicular lines intersect at a 90 degree angle because their slopes are _________ _____________, while parallel lines never intersect because their slopes are ____ ____________.
opposite reciprocals
the same
What is a rotation?
A transformation that locates points in the same direction along concentric circles and through the same angle of rotation around the center of rotation.
What is the transformation below?
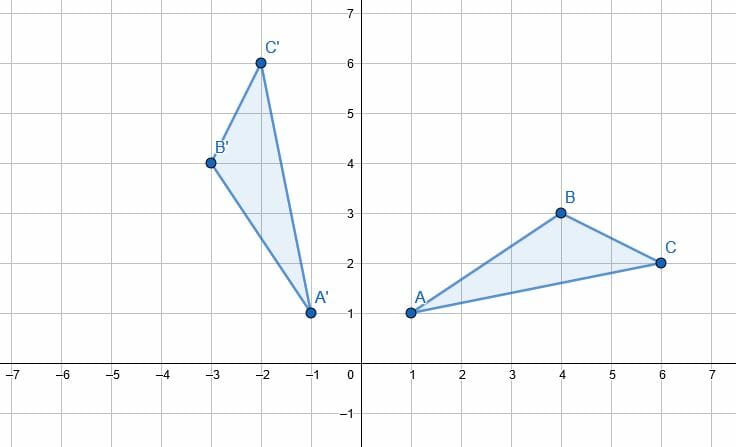
Rotation 90 degrees counterclockwise around the origin (0,0)
Draw all lines of symmetry for the regular polygon again, then list the angles satisfying its rotational symmetry.
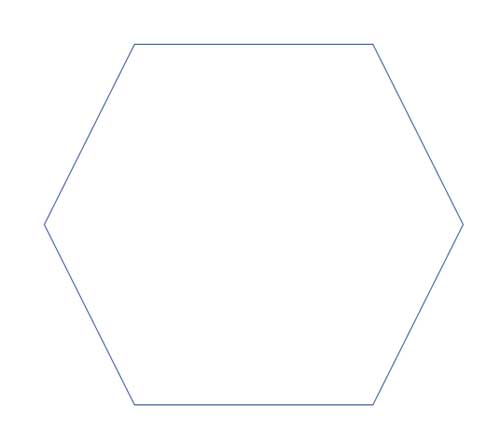
(lines of symmetry through each vertex, 5 lines)
72, 144, 216, 288, 360
Prove, with transformations, that BC is congruent to AE

Rotation and reflection
Reflection and translation
Create an equation that is parallel to y= 3/5x+7
y=3/5x + b
(b is any number)
What is a reflection?
A transformation that locates points across a line of reflection so that the line of reflection is a perpendicular bisector of each line segment connecting corresponding pre-image and image points.
Determine the transformation and write the rule.
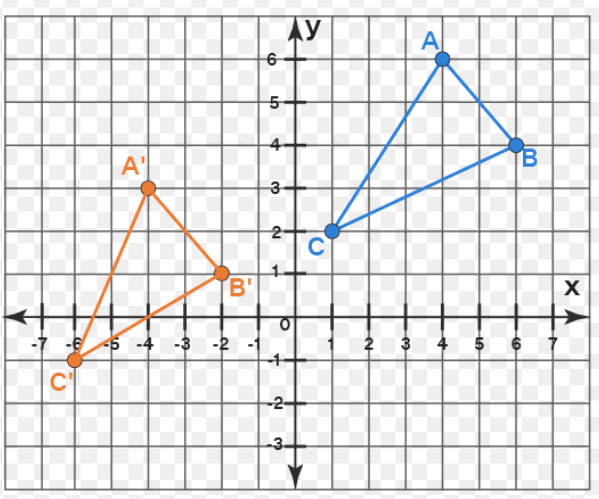
translation
f(x,y)= (x-8, y-3)
Draw the lines of symmetry for the equilateral triangle below. Then list the angles satisfying its rotational symmetry.
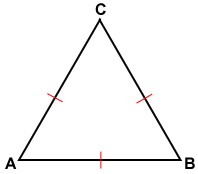
3 lines
60, 120, 180
How can you prove, with transformations, that the two figures are congruent?

translation doesn't change side length or angle measure, therefore the measure of angle A is the same as A', which applies to all angles and side lengths.
Create the equation of a line that is perpendicular to the line given below
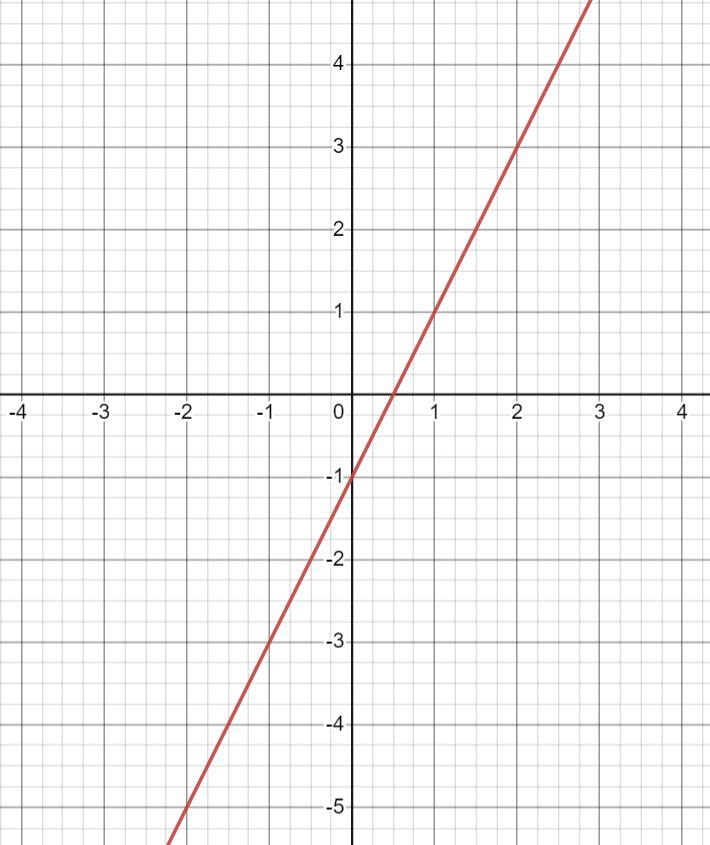
y= -1/2x (+ or - any b)
What is a rigid transformation?
Any transformation that will preserve distance and angle measure of a figure.
The coordinates for triangle ABC is A(-2,0) B(0,4) C(-4,3).
What would the coordinate points be for triangle A'B'C' when the function rule f(x,y)= (-y,x) is used?
A' (0,-2)
B' (-4,0)
C' (-3,-4)
If my rotational angles are multiples of 30 (i.e. 30, 60, 90, 120,...360)
How many sides of the regular polygon are there?
12
360/12=30
Prove, with transformations, how DA is congruent to AB

Reflection over CA
Find the equation of the given line, create an equation of a line parallel to the given line, AND create an equation that is perpendicular to the given line. 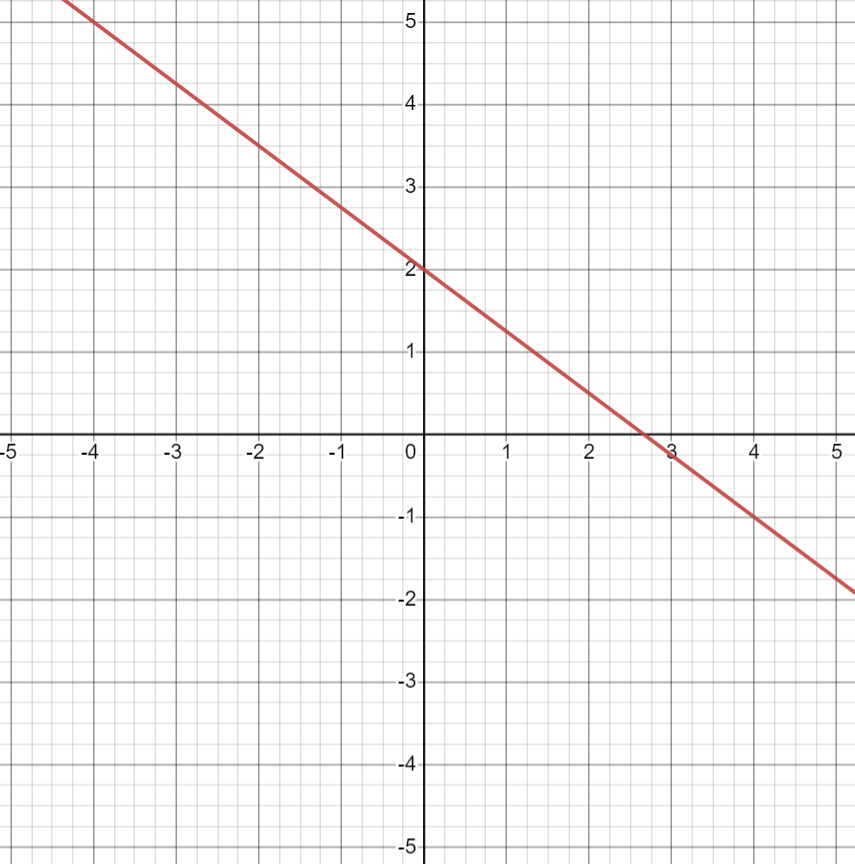
given line: y= -3/4x+2
parallel: y=-3/4x (+ or - any b value)
perpendicular: y=4/3x (+ or - any b value)
