Exponential Growth & Decay
Logarithms
Properties of Logs
Solving Logs
Mix
100
Determine whether the relation is a function and explain why
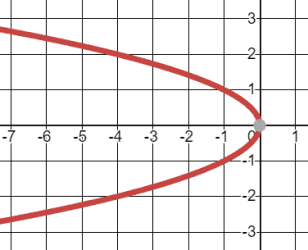
No, does not pass the Vertical Line Test
100
Identify the function family.
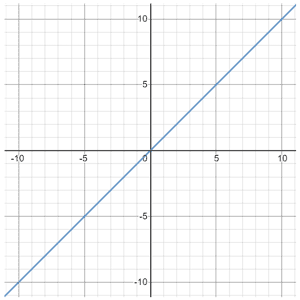
Linear
100
Describe the transformation.
f(x) = x-3
Vertical shift 3 units down
100
Where the graph comes to a point is called the
Vertex
100
A piecewise function is make up of distinct "______" depending on rules assigned for the _______.
pieces, domain
200
Is the set of ordered pairs a function?
{(2,10)(3,10),(4,10),(5,10)}
Yes
200
Identify the function family.
Constant
200
Describe the transformation(s).
f(x)= (x-7)2+13
Horizontal shift 7 units right
Vertical shift 13 units up
200
In vertex form, what does a, h, and k represent
a = slope
h = moves graph L/R
k = moves graph Up/Down
200
What is the domain of f(x)= -2
Domain: x ≥ -2
300
State the domain and range.
{(0,7),(0,8),(1,7),(1,8),(1,9),(2,10)}
Domain: {0,1,2}
Range: {7,8,9,10}
300
Identify the family function.
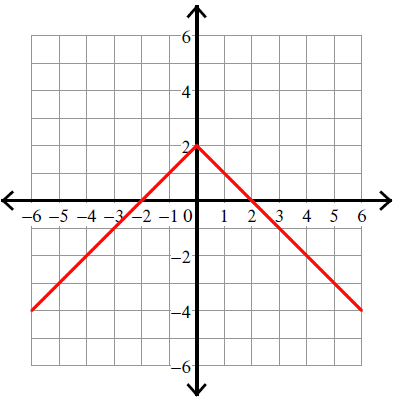
Absolute Value
300
Describe the transformation(s).
f(x) = -5/3x
Reflection over the x-axis
Vertical stretch by a factor of 5/3
300
Write the absolute value function given the transformation
let f(x) = |x|
Vertical stretch by a factor of 4
g(x) = 4|x|
300
Evaluate f(-1)
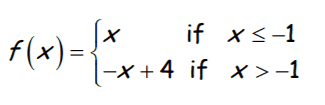
-1
400
State the domain and range
Domain: −1<x<1
Range: 0≤y<1
400
Identify the family function.
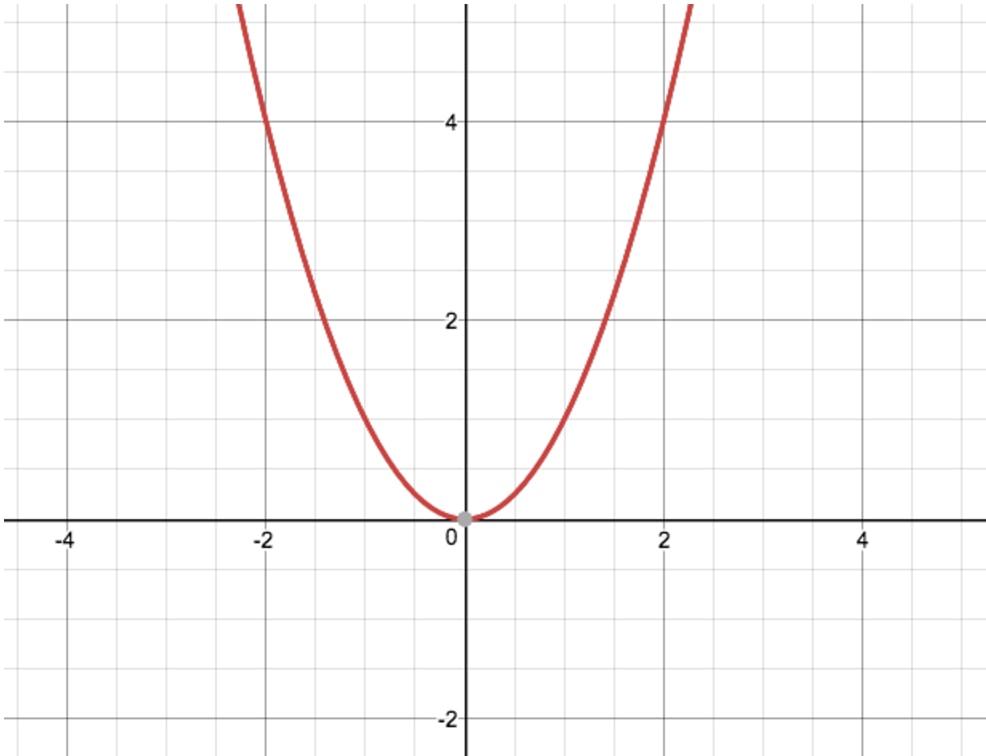
Quadratic
400
Describe the transformation(s).
f(x)= 1/2 |x+2|
Vertical shrink by a factor of 1/2
Horizontal shift 2 units left
400
Write the absolute value function given the transformation
let f(x) = |x|
Horizontal stretch by a factor of 5
g(x) = |1/5x|
400
Write a rule for the graphed piecewise function.
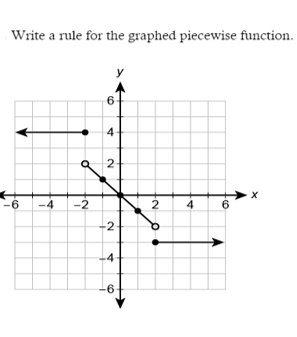
f(x) = {4, x≤-2
-x, -2 < x < 2
-3, x ≥ 2
500
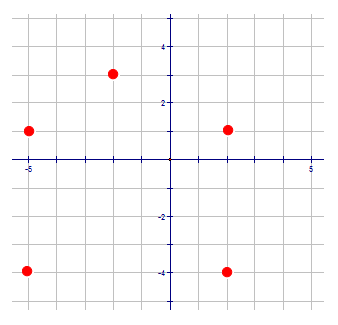
State the domain and range.
Domain: {-5, -2, 2}
Range: {-4, 1, 3}
500
What are the maximums and minimums of a constant function?
None
500
Describe the transformation(s).
f(x) = -7x2 + 11
Reflection over the x axis
Vertical stretch by a factor of 7
Vertical shift 11 units up
500
Write the absolute value function given the transformation
let f(x) = |x|
Horizontal shrink by a factor of 1/9
g(x) = |9x|
500
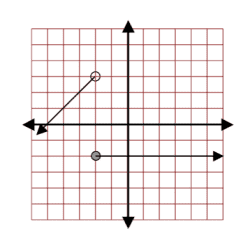
Graph f(x) = { x, x>1
-2x+3, x ≤ 1