Slope
Writing Equations
Distance/Perimeter/Area
Random
100
What is the slope of the line that passes through the points (1,−1) and (−8,−7)?
m=2/3
100
Put the following equation of a line into slope-intercept form, simplifying all fractions.
9y - 3x =18
y= 1/3x+2
100
Find the distance between the two points. Round to the nearest tenth.
(−8,0) and (−4,2)
4.5 units
100
Solve for x:
7x =−4x−6(−x−5)
x = 6
200
What is the slope of the line that passes through the points (9,−10) and (14,5)?
m=3
200
Write the equation of the line that has a slope of ⅔ and passes through the point (6, 3).
y=-2/3x -1
200
Find the distance between the two points. Round to the nearest tenth.
(−9,9) and (−3,2)
9.2 units
200
Find the slope of the line represented by the equation below.
−12 = 3y−4x
m = 4/3
300
Find the slope of a line parallel to the line whose equation is 10x + 12y =-120. Simplify.
m= -5/6
300
Find the equation of the line that passes through the points (-2, 1) & (3, 6).
y=1x+3
300
Find the area.
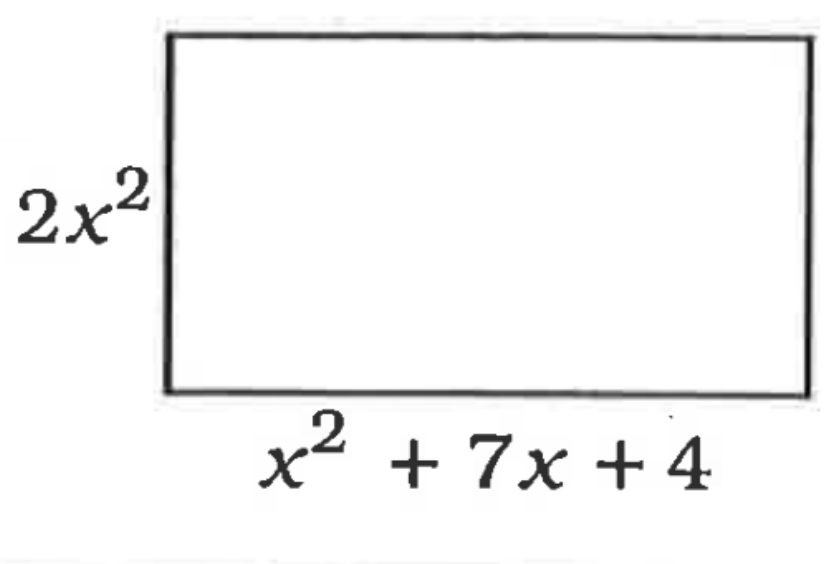
2x4+14x3+8x2
300
Given J(−6,−5), K(−2,−6), L(3,−2), and M(x,0). Find x such that JK ∥ LM.
x =-5
400
Find the slope of a line perpendicular to the line whose equation is 5x+y=−4. Fully simplify your answer.
400
What is an equation of the line that passes through the point (−3,−8) and is parallel to the line 4x−y=4?
y=4x+4
400
Find the perimeter of the triangle. Round to the nearest tenth.
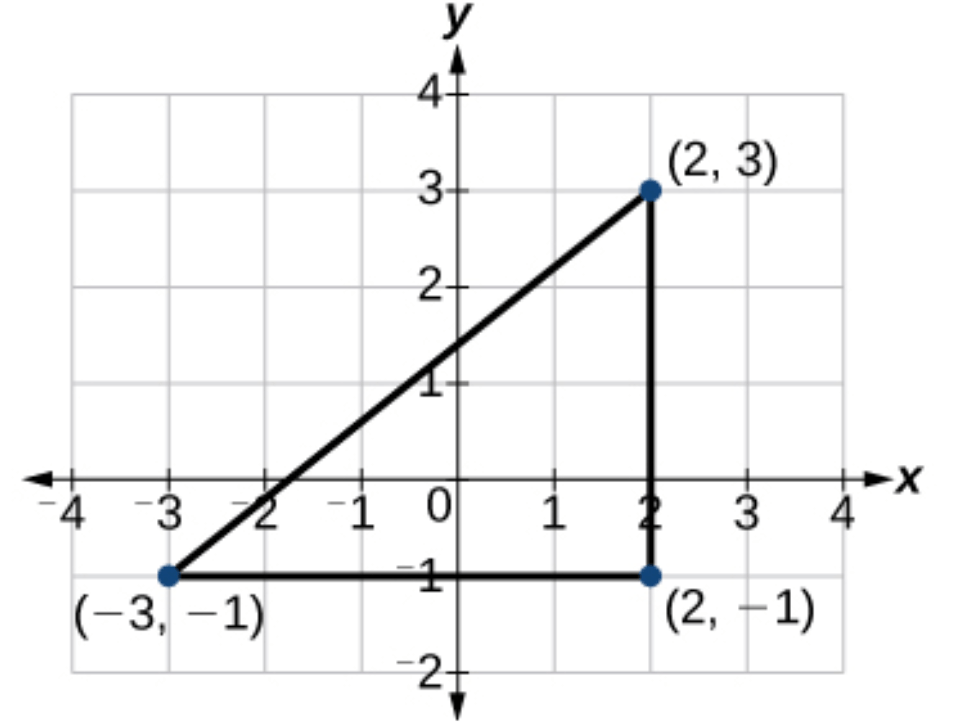
15.4 units
400
Multiply the polynomial:
(−x+4)(3x2−2x−7)
3x3+14x2−x−28
500
For the function f(x)=x2 +10. Find the slope of the secant line between x=−3 and x=−1.
m = -4
500
Find an equation for the perpendicular bisector of the line segment whose endpoints are (−7,−9) and (1,3).
y= −2/3x−5
500
Find the perimeter of the triangle. Round to the nearest tenth.
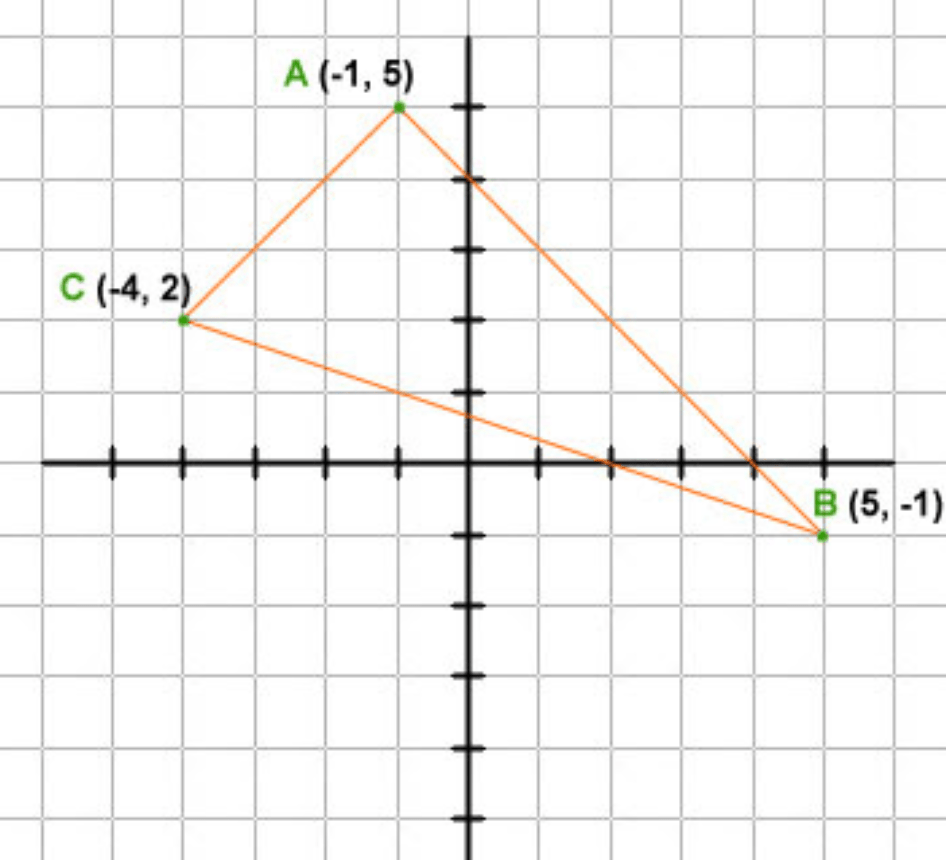
22.2 units
500
Find the area of the shaded region.
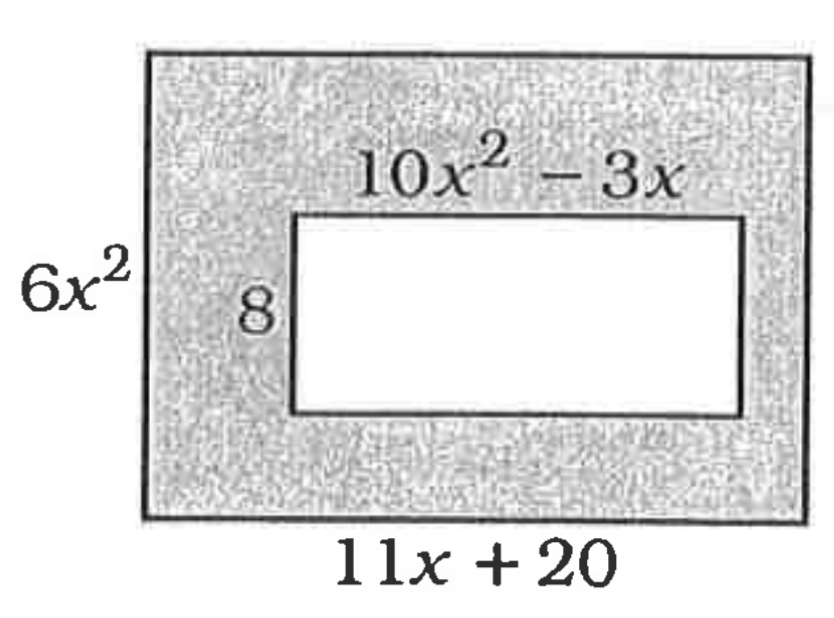
66x3+ 40x2+24x