Missing Angles / Transformations
Prove This!
Triangle Congruence Theorems
Name that Reason
100
If DB bisects ∠B, what is the degree measure of ∠DBC?
What is 52 degrees.
100
How do we know that ∠AEC ≅ ∠DEB below?
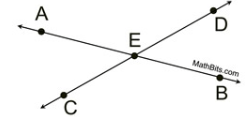
What is Vertical Angles?
100
If three sides of one triangle are congruent to three sides of another triangle, then these two triangles are congruent.
What is the Side-Side-Side Triangle Congruence Theorem.
100
What is the "Reason" for Statement #1 below?
What is "given"?
200
In parallelogram ABCD, the measure of angle A is 99 degrees. What is the measure of angle B?
What is 81 degrees ?
Opposite angles in a parallelogram are congruent, therefore 99+99= 198
All four angles in a quadrilateral add to 360 degrees
360 - 198 = 162
There are two remaining angles that are congruent to each other, therefore 162 /2 = 81
Angle B must be 81 degrees
200
How do we know that segement CA ≅ segment CA below?
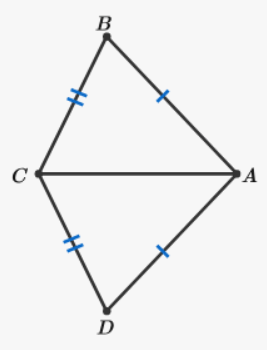
What is the Reflexive Property?
200
What triangle congruence theorem can be used to prove triangle VXY is congruent to triangle VWY.
What is the Side-Angle-Side Triangle Congruence Theorem.
200
What is the reason for statement #3 below?
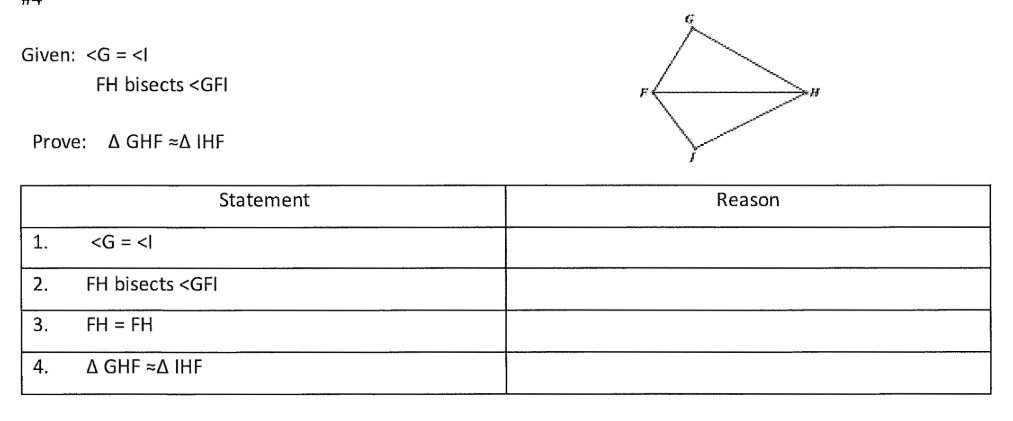
What is the Reflexive Property?
300
Triangles ACD and BCD are isosceles. Angle BAC has a measure of 18 degrees and angle BDC has a measure of 48 degrees. Find the measure of angle ABD.
What is 138 degrees
18 + 18 = 36.
180-36 = 144
So base angles of ADC are each ½ of that.
144-96 = 48
So angle ADB is 24
24 + 18 = 42
180-42 = 138
300
ABCD is a parallelogram. If the length of AB is 7.3 cm, what is the length of segment CD?
What is 7.3 cm?
300
If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then these two triangles are congruent.
What is the Angle-Side-Angle Triangle Congruence Theorem
300
What is the reason for statement #3 below?
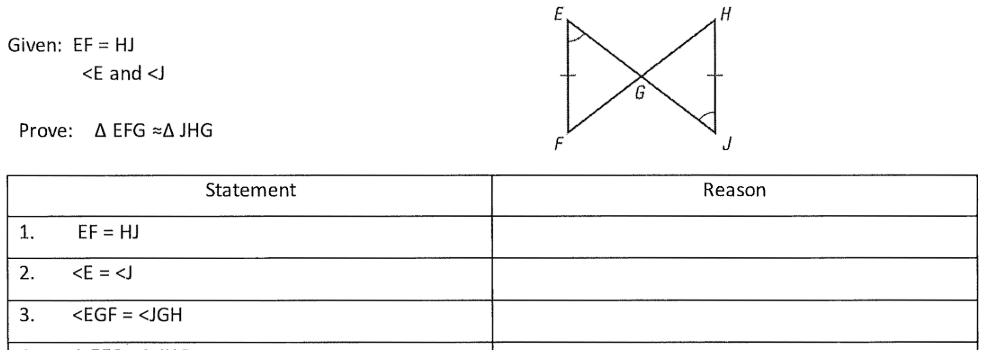
What is Definition of Vertical Angles?
400
Triangle A′B′C′ is a rotation of triangle ABC by 60 degrees using Q as the center. Select all statements that MUST be true.
a) Angle ABC is 60 degrees.
b) Angle AQA′ is 60 degrees.
c) Points C and C′ coincide.
d) Triangles ABC and A′B′C′ are congruent.
e) Angle ABC is congruent to angle A′B′C′.
f) Segment BC is congruent to segment B′C′.
What is B, D, E, and F?
400
In the triangle below, if D is the midpoint of segment AC, what is segment AD congruent to?
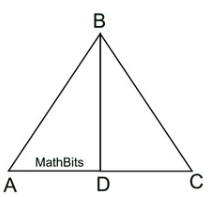
What is segment CD?
400
By what triangle congruence theorem proves these two triangles are congruent?
What is the Side-Side-Side Triangle Congruence Theorem.
400
What is the reason for statement #2 below?
Given: EF // HJ
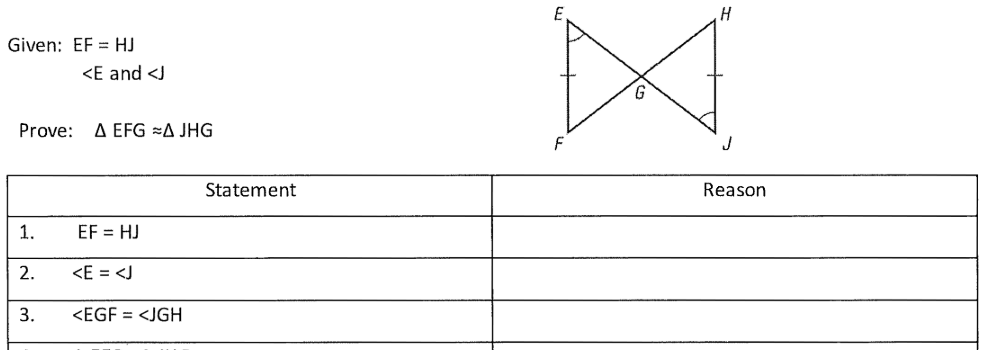
What is Alternate Interior Angles?
500
Triangle A′B′C′ is a reflection of triangle ABC across line ℓ. Select all statements that MUST be true.
a) Line ℓ bisects segment AB.
b) Angle ABC is 60 degrees.
c) Line BB′ is perpendicular to line ℓ.
d) Angle ABC is congruent to angle A′B′C′.
e) Triangles ABC and A′B′C′ are congruent.
f) Segment BC is congruent to segment A′C′.
What is C, D, E
500
Figure KLMN is a parallelogram. Prove that triangle KNL is congruent to triangle MLN.
500
What triangle congruence theorem can be used to prove triangle ABC and triangle XYZ are congruent?
What is the Side-Side-Side Triangle Congruence theorem.
We can use the Pythagorean Theorem to find the length of the missing side.
Since all other sides are equal in length, the missing side should also be equal in lenght.
500
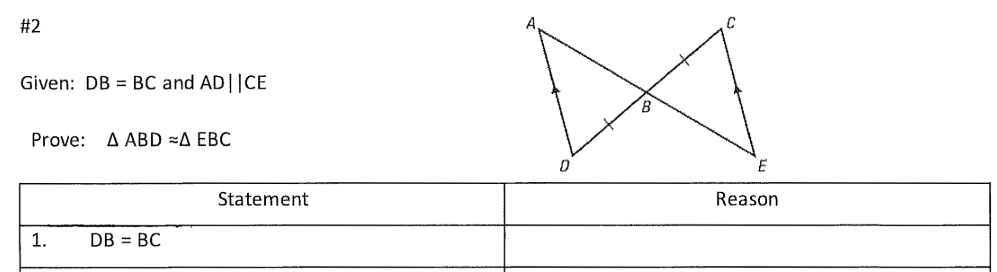
In the triangles below, AD || CE. Name 2 angles that must be congruent.
hint: DC and AE are transversals
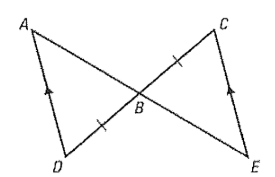
What is A and ∠E OR ∠D and ∠C?
(Alternate interior angles)