Different Function Families
Different f(x) fam pt. 2
Quadratics
Quadratics Applications
Review
100
Using the general graphing form, what transformations are represented by the:
- 'a' - value
- h - value
- k value
- a: Reflections, stretches/compressions
-h: horizontal shifts
-k: vertical shifts
100
The graph of this function
y=0.3(x-7.66)^2 +1700
will have a: maximum/minimum value.
We know this because: ___
The graph of this function will have a minimum value at the vertex. We know this because the "a"-value is positive.
100
What is the quadratic formula? When you solve it, what does it tell you about the parabola?
The quadratic formula tells you the x-intercepts (or roots) of the parabola.
100
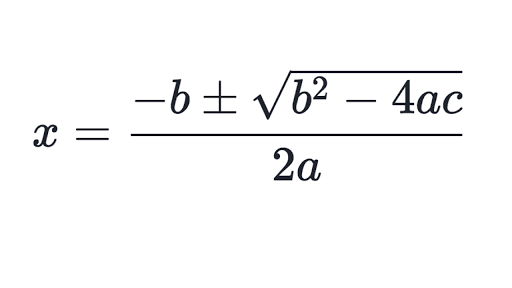
After t seconds, height, h (in feet) of a rocket, is given by the formula.
h(t)=-10t^2+25t
What is the height after 1.5 seconds?
15 feet
100
1) What is the equation for a circle with center at the origin?
2)What is the equation of a circle not at the origin?
1)
x^2 +y^2 = r^2
2)
(x-h)^2 + (y-k)^2 = r^2
200
Name each function type:
a)
f(x)=-3x^2+6
b)
f(x)= sqrt(x-12) -1
c)
f(x) 2*3^x
d)
f(x)=1/(x+3)
a) quadratic function
b) square root function
c) exponential function
d) reciprocal function
200
Your IG follower count grows by 5% each month. If you have 106 followers right now, how many followers will you have in 6 months?
142 followers
200
Solve for the x- and y- intercepts of
9x-7y=3
x=1/3 , y=-3/7
200
After t seconds, height, h (in feet) of a rocket, is given by the formula.
h(t)=-10t^2+25t
What is the maximum height? What was the time that it reached that height?
It took 1.25 seconds to reach a maximum height of 15.63 feet.
200
Simplify
sqrt(156)
2sqrt(39)
300
Given the function,
f(x)= -1/2|x|-6
Determine how the function differs from the parent function.
This function is different its from the parent function because it is compressed by a factor of 1/2, it is reflected across the x-axis, and it is shifted down 6.
300
Sketch the graph of the function and list 3 points:
f(x)=-|x+2|+1
Possible Points:
(-2, 1), (-1,0), (0,-1), (1,-2), (2,-4)
300
Factor the quadratic:
x^2-13x+42
(x-6)(x-7)
300
The launch of a hair tie can be modeled with the equation
where d is distance in centimeters and t is time in seconds. What is the maximum height of the hair tie and when does it occur?
d(t)=-2(t-7)^2+30
Hair tie reaches 30 cm high after 7 seconds.
300
Give the domain and range of the RED graph:
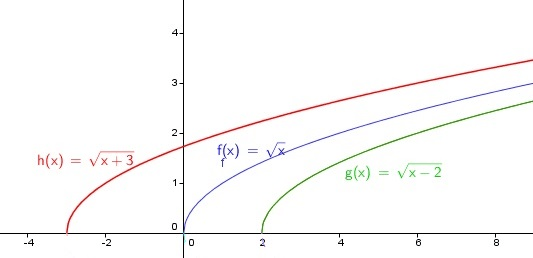
D:
-3 </=x < "infinity"
R:
0 </= y < "infinity"
400
Give a sketch for the following function families and write the parent graph:
1) Square Root Function 2) Absolute Value Function 3) Cubic Function
1)
f(x)=sqrtx
2)
f(x)=|x|
3)
f(x)=x^3
400
The price of a movie ticket averages $10.25 and is increasing by 3% per year.
Write a function that represents the cost of a movie ticket n years from now.
If tickets continue to increase at the same rate, what will they cost 10 years from now?
1.
f(x) = 10.25(1.03)^x
2.
$13.78
400
For the function
t(x)=-3x^2-11x+4
Determine for what values does t(x) = 0.
t(x) = 0 when
x=-4 or x=1/3
400
How do you know when a function is a quadratic?
When the degree of the function (the highest exponent) is 2.
(When x is squared)
400
given that b=3.5, which trig ratios (Sin, Cos, Tan) could be used to find the length of the side c ?
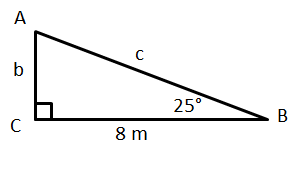
Sin and Cos
500
Give a sketch for the following function families and write the parent graph:
1) Linear Function 2) Reciprocal Function 3) Exponential Function
1)
f(x)=x
2)
f(x)=1/x
3)
f(x)=a*b^x
500
** DOUBLE JEOPARDY**
Given the parent graph below, Sketch a function for a transformation of the graph that has been reflected, moved to the right 3 units, and moved down 4 units. Then, write the equation for the new graph.
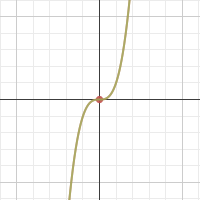
f(x)=-(x-3)^3-4
500
Solve the quadratic function:
2x^2-5x = 12
x=-3/2 or 4
500
Maura uses her green garden hose to water her garden. The greatest height the water reaches is 8 feet, and it lands on the plants 10 feet from where she is standing. Both the nozzle of the hose and the top of the flowers are 4 feet above the ground.
Sketch the scenario and write an equation that models the path of the water.
y=-4/25(x-5)^2+8
500
Simplify:
1)
(2sqrt8)^2
2)
sqrtx + sqrty +5sqrtx + 2sqrty
1)
32
2)
6sqrtx + 3sqrt y