y=7
Solve y=x+9 when y=-10
x=-19
What is an equation that models the following table?
y=4x+3
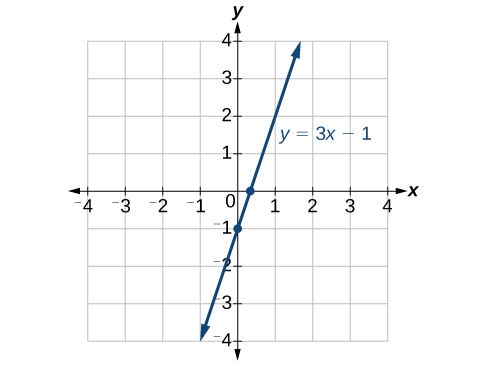
Graph the following equation on the provided grid paper:
y=3x-1
A math class wanted to research if study time affected overall math grades. The data is below:
What is the trend of the data?
Positive
As study time increases the overall math grade increases.
Evaluate y=3x-4 when x=-5
y=-19
Solve y=-5x+2 when y=37
y=-7
What is the equation that models the following graph?
y=2/3x+2
Graph the following equation on the provided grid paper:
y=4x+5

If the equation of the trend line that best fits this data is y=7.5x+55, what does each piece of the equation represent?
Y --> Math Grade (percent)
X --> Study Time (hours)
Slope --> Increase of 7.5% grade per 1 hour of studying.
y-intercept --> 55% grade with no studying.
Evaluate y=1/4x-9 when x=12
y=-6
Solve y=1/4x+3 for y=-1
Write an equation that models the following table:

y=2.5x-5
Graph the following equation on the provided grid paper:
y=-5/3x+10

If the equation of the trend line that best fits this data is y=7.5x+55, what would you expect someone's grade to be if they studied for 4.5 hours?
y= 88.75%
f(6)=4/3x+10
f(x)=18
Solve y=-2/7x+6 for y=10
x=-14
What is an equation of the following graph?
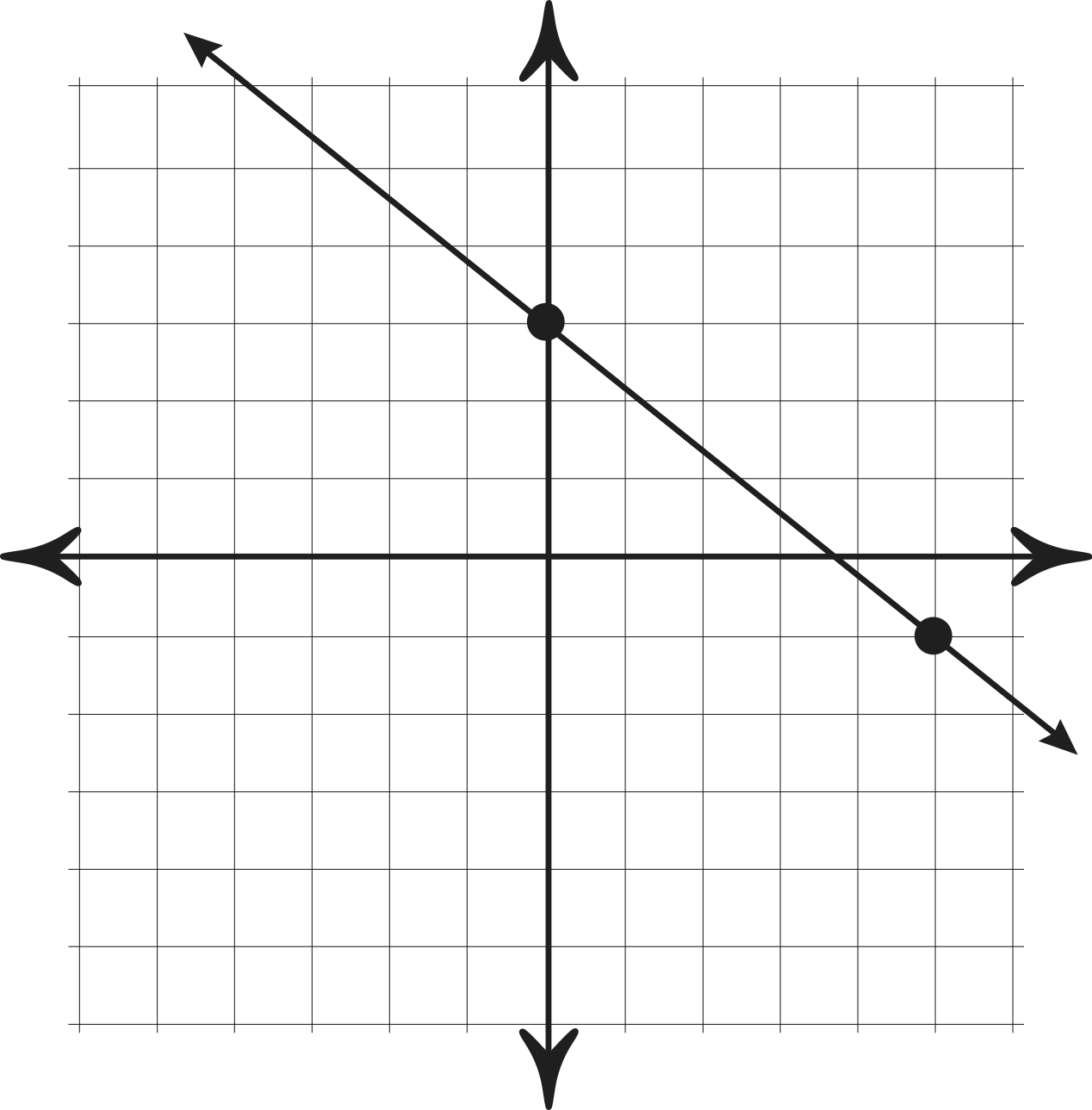
y=-4/5x+3
Graph the equation x=3 on the given grid paper.

If the equation of the trend line that best fits this data is y=7.5x+55, How long did someone study if they got 99%?
x=5.87 hrs.
f(x)=23/2 or 11 1/2
Solve y=3(-2x+8) for y=6
x=3
What is an equation of a line that goes through the following two points?
(3, -7) & (5, -1)
y=3x - 16
Graph the following equation on the provided grid paper:
12=2x+3y
A math class wanted to research if study time affected overall math grades. They hypothesis is as follows:
Hypothesis: If students study for at least 1 hour then they will at least get a passing score.
Is this hypothesis correct? Why or why not?
Trendline: y=7.5x+55
Yes the hypothesis is correct because if a student were to study for 1 hour then they would average a grade of 62.5% which is a passing grade.
