Convert to degrees
(11pi)/20
99 degrees
Identify the coordinate on the unit circle for the value
(5pi)/4
(-sqrt(2)/2,-sqrt(2)/2)
The quadrant containing points (-x,-y)
Quadrant 3
P(4, 1) is a point on the terminal side of \theta in standard form. Find the exact value of
tan\theta write in simplified form
tan\theta=\frac{1}{4}
-2+sin\theta=-3
\frac{3\pi}{2}
The arc length intercepted by an angle with radius 9 and degree measure of 160.
8\pi or 25.13
Find
sin(pi)
0
If you have a radian degress measure with a denominator of 6, what angle of a special right triangle should you be referencing?
30
(-4,2) is a point on the terminal side of \theta . Find \cos\theta. Write in simplified form.
-\frac{2\sqrt{5}}{5}
3-4cos\theta=7-2cos\theta
No solution
Find a angle measurement that is coterminal with
\frac{5pi}{3} in radians
Possible answers:
...-\frac{7pi}{3},-\frac{pi}{3},..., \frac{11\pi}{3},\frac{17\pi}{3}...
Identify the error with this unit circle.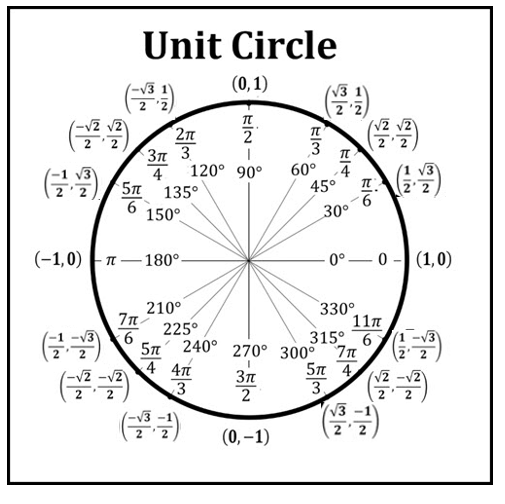
The 30 degree and 60 degree coordinates are switched
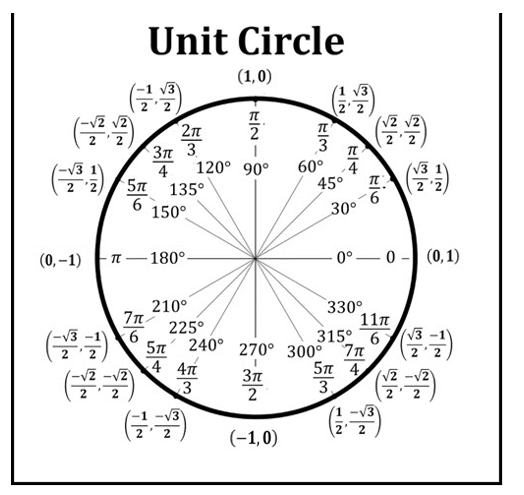
Identify the error in this unit circle
The coordinates of the axes
Identify the quadrant where \theta lies if the following statements are true:
cos\theta>0, csc\theta<0
Quadrant IV
0=-4-4\sec\theta-sec^2\theta
\frac{2\pi}{3}, \frac{4\pi}{3}
Find the area of a sector of a circle that has a radius of 6 meters and a measure of \frac{2\pi}{3} radians.
12\pi or 37.7 m^2
Evaluate
sec((-4pi)/3)
-2
tan((7pi)/2)
undefined
If csc(x)=5/4 and tan(x)<0, find cot(x)
cot\theta=-\frac{3}{4}
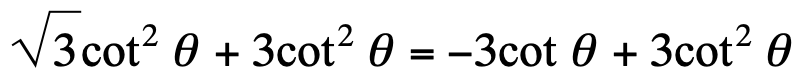
\frac{\pi}{2},\frac{5\pi}{6},\frac{3\pi}{2},\frac{11\pi}{6}
If cosine of x is -2/3 and cotangent of x is positive, which quadrant does x lie in?
Quadrant 3
\cot(\theta)=-\sqrt{3} for 0°\le\theta<360°
150° and 330°
\csc\frac{16\pi}{3}
(-2sqrt(3))/3
If secx=-\frac{\sqrt{65}}{4} and csc(x)<0, find tan(x)
\frac{7}{4}
\frac{\sin^2x-9){sinx-3)=2
x=\frac{3\pi}{2}