Differentiation Easier
Differentiation Harder
Inverse Functions and Calculator Stuff
Tangent Lines
Applications
Other Stuff
100
f(x) = x3 - 5x
f'(x) = ??
f'(x) = 3x2-5
100
y = (5x2+3x)(x2-3x+2)
Find y'
*Product Rule or multiply it out into a polynomial first
y' = (10x+3)(x2-3x+2)+(5x2+3x)(2x-3)
y' = 20x3-36x2+2x+6
100
f(x) = cos-1(2x). Find f'(x)
f'(x) = (-2)/sqrt(1-4x^2)
100
Find an equation of the tangent line to the graph of f(x) = (x-4)10 at the point where x = 5
Final Answer: y = 10(x-5)+1 (in point slope form)
Why? f(5) = 1 (point)
f'(x) = 10(x-4)9
f'(5) = 10(1)9 = 10 (slope)
100
How are acceleration, position, and velocity related?
velocity is the derivative of position.
acceleration is the derivative of velocity or the second derivative of position
100
Find all the points where the function is discontinuous. What type of discontinuity is it?
f(x) = (x^2-16)/(x+4)
point discontinuity at x = -4. There is a hole at (-4,-8)
200
Find the derivative of
y = 4root3(x) - 6sqrt(x)
y' = 4/3*x^(-2/3) - 3*x^(-1/2)
200
differentiate y = log3(x-5)
y' = 1/(ln3*(x-5))
200
find the derivative of
y = sin^-1sqrt(1-x^2)
y' = (-x)/(absxsqrt(1-x^2)
200
Find the x-coordinates of all points on the graph of y = x3 - 4x2 + 5x at which the tangent line is horizontal.
horizontal tangent line means slope = 0.
slope = derivative.
y' = 3x2 - 8x +5
0 = 3x2 - 8x +5 = (3x-5)(x-1)
x = 5/3, 1
200
What's the difference between speed and velocity?
speed is the absolute value of velocity. It does not give direction while velocity does.
200
Given f(x) = x3 - 5x, Find the average rate of change of f(x) between x = 1 and x = 5
f(1) = -4
f(5) = 100
AROC = (100--4)/(5-1) = 104/4 = 26
300
Find the derivative of y = e-5x
y' = -5e-5x
300
If 6x2+8xy + y2 = 6, find y'
dy/dx = y' = -(6x+4y)/(4x+y)
300
Let f be the function f(x) = ln(3x2). For what value of x is the slope of the line tangent to the graph of f at (x,f(x)) equal to 3?
x = 2/3
Why? graph f'(x) and the line y = 3. Find the intersection of the two graphs. You don't even need to calculate the derivative, the calculator can graph derivatives.
300
Find the x-coordinates of all points on the graph of y = x3 - 4x2 + 5x at which the tangent line is parallel to the line 2y - 10x - 7 = 0.
line 2y - 10x - 7 = 0 --> y = 5x - 7/2 --> slope = 5
derivative of graph: y' = 3x2 - 8x + 5. Set this equal to 5 and solve for x
x = 0, 8/3
300
If a ball is dropped from a cliff 800ft above the ground, the distance of the ball above the ground is given by f(t) = 800 - 16t2 where t is given in seconds. Find the acceleration of the ball at t = 3 seconds
f(t) is position function. f''(t) would be the acceleration function. f'(t) = -32t and f''(t) = -32. So no matter what the time is, the acceleration of the ball will be -32 ft/sec2
300
Find the limit of f(x) as x approaches the point of discontinuity.
f(x) = (x^2-16)/(x+4)
-8. Why? There is a hole at (-4,-8) so the limit as x approaches -4 would be the y-value of the hole.
400
find the derivative: y = (lnx)2
y' = 2lnx*1/x = (2lnx)/x
400
Find the derivative of g(x) = 3cotx
g'(t) = ln3*3cotx*-csc2x
400
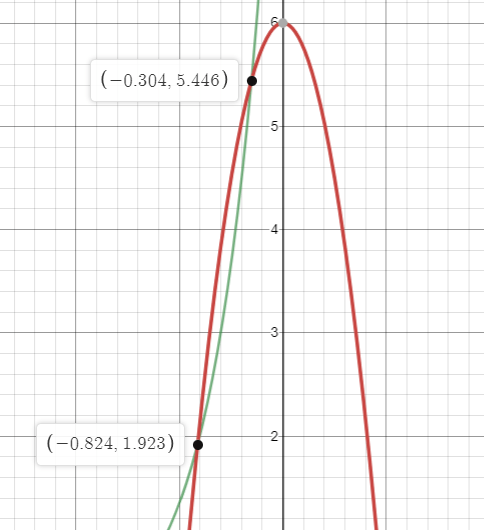
Let f be the function given by f(x) = 5e2x and let g be the function given by g(x) = -2x3+6x. At what value of x do the graphs of f and g have parallel tangent lines?
x = -0.304 and -0.824.
Why? Graph the derivatives of each function. Since parallel, looking for where slopes (aka derivatives) are the same. Find the two intersection points.
400
Find the values of x where the given function has a vertical tangent line.
y = root3(x+1) + 5
x = -1
Why? Take the derivative and set the denominator equal to 0. Solve for x.
y' = 1/(3(root3(x+1))^2)
400
1/e^2
Why?
H'(x) =f'(x)*e^(f(x))*g(x) + e^(f(x))*g'(x)
400
Find s'(t) given s(t) = 8-2t
ln8*8-2t*-2
s'(t) = -2(8)-2tln8
500
find g'(x) if
g(x) = (3x+1)/(2x-5)
g'(x) = (-17)/(2x-5)^2
500
If 4x2+y2 = 6, then find y''.
y'' = (-4y^2-16x^2)/y^3
Why? implicit differentiation
8x + 2yy' = 0
y' = -4x/y
y'' = (-4y+4xy')/y2 --> substitute y' into the equation and simplify.
500
Find an approximate equation for the line tangent to the graph of f(x) = x6+5x4+1 at the point where f'(x) = 2
y = 2(x-0.455)+1.223
1. Find the point where f'(x) = 2 by graphing f'(x) and the line y = 2. Find the intersection point. (x = 0.4549318844)
2. Find the y value for this point by doing f(0.4549...) to get y = 1.223033447
3. already given slope in the question. f'(x) = 2
500
Find the equation of the tangent line of x2y-y3 = 8 at the point (-3,1)
y = (x+3)+1
Why? implicitly differentiate then plug in the given point to get the slope. Use that slope and point to get the equation of the tangent line
2xy+x^2(dy)/(dx) - 3y^2(dy)/(dx) = 0
(dy)/(dx) = (2xy)/(3y^2-x^2)
500
1/4
K'(x) = -2(fg)-3*[f'g+fg'}
500
If f(x) = (sinx - cosx)2, find the equation of the normal line to the graph of f through the point (0,1)
y = 1/2x+1
Why? f'(x) = 2(sinx-cosx)(cosx+sinx) = 2(sin2x - cos2x)
f'(0) = 2(sin0 - cos0) = 2(0-1) = -2
normal line = perpendicular --> slope = 1/2
already given y intercept