Perpendicular Bisector
Altitude
Shortest Distance
100
What is another name for Perpendicular Bisector
Right Bisector
100
What is another name for altitude?
Height
100
What is the formula for distance
200
Define and Draw a perpendicular bisector
Line perpendicular to the line segment and divides the line segment into two equal parts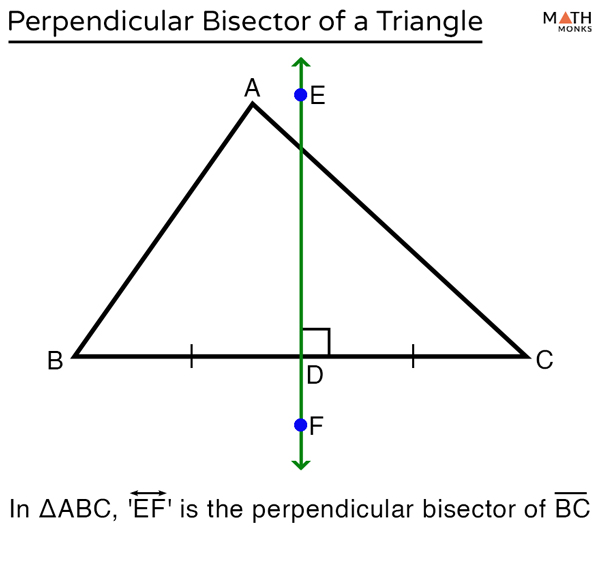
200
Define and Draw an altitude
A line segment that goes from the vertex of a geometric shape, perpendicular to the opposite side.
200
What is the shortest distance from a point to a line segment?
The length of a line segment that is perpendicular to the line, connecting to the point.
300
What are the steps to solve for a perpendicular bisector?
1. Find the midpoint of the line segment
2. Find the slope of the line segment, then find the negative reciprocal.
3. Sub midpoint and negative reciprocal slope into y=mx+b to solve for b.
4. Rewrite y=mx+b using the new m and b
300
What are the steps to solve for an altitude?
1. Find the slope of the side opposite to the vertex
2. Find the slope of the perpendicular line using negative reciprocal slope.
3. Substitute the vertex (x,y) and the negative reciprocal slope into y = mx+b to solve for b.
4. Rewrite equation by subbing in m and b to y=mx+b.
300
What are the steps to find the shortest distance?
1. Find the equation of line
2. Find the slope and then find the perpendicular slope using the negative reciprocal.
3. Use the negative reciprocal slope and the point to substitute into y=mx+b to solve for y-int. Rewrite y=mb+b for new line.
4. Use elimination or substitution to find the POI.
5. Find distance using the formula from the point to the POI.
400
Determine the equation of the line that is perpendicular to the line passing through the points A(3,7) and B(5,-4) and passing through the midpoint of line segment AB. (explain your steps)
y = 2/11 x + 17/22
400
Triangle FGH has vertices F(4,5) G(-3,2) H(5,-2). Find the equation of the altitude from vertex G.
y = 1/7 x + 17/7
400
Find the shortest distance from point C (4,-2) to the line passing through A (1,3) and B (-4,-2)
The shortest distance is root 32
500
Given triangle LMN where L is at (4,4), M is at (8,6), and N is at (2,3) calculate the right bisector of LM.
y = -2x +17
500
Considering triangle ABC where A is (-3,-2), B is (-1,5) and C is (4,3) find the equation of the line for the altitude from vertex B.
y = -7/5 x + 18/5
500
Adam is planning to build a new school in a city. He wants to ensure that the school (4,5) is located as close as possible to a straight road running east-west. Two points on the road are B(2, 6) and C(6, 2). What is the shortest distance Adam needs to consider for constructing the school? (Round to 2 decimal places)
Approx 0.71 Units.