3.1 Using Variables to Represent Problems
3.2 Graphing Inequalities & Feasible Regions
3.3 Reasoning Based on Graphs
3.4 Solve Systems of Equations and Inequalities
Vocabulary
100
You went out to eat with a group of your friends, in total there were 12 people. Everyone either ordered a slice of pizza or a burger. Pizza slices are $2 and Burgers are $3. The total your group paid was $27. Define variables and write down the system of equations for how many slices of pizza and many burgers did you order?
b = # of burgers
P = # of pizza slices
b + p = 12
3b + 2p = 27
100
Graph this inequality
r > 2
100
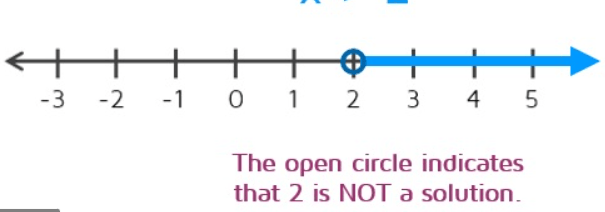
Based on the graph, what is the solution to the system of equations?
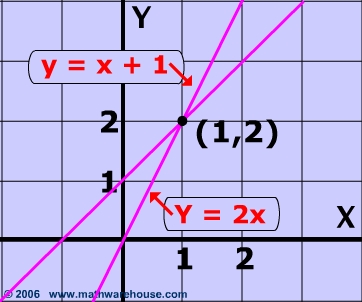
Point of Intersection (1, 2)
100
Solve the system
y = 4x - 6
y = 8x - 18
(3, 6)
x = 3 y = 6
100
What is the feasible region?
The region on the graph of system of inequalities that shows where all constraints are met / satisfied.
200
There are at least as many students as teachers at the Student Council movie night.
s>=t
200
Graph the inequality
k<=-2
200
In a system of inequalities, which coordinates or combinations would give the max profit?
Corner points
200
Solve the inequality
-3(2x - 1) > 15
x < -3
200
Where is a solution to a system of equations located on the graph?
Point of Intersection
300
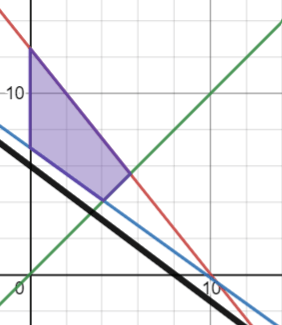
The knitting club is making scarves and hats for a fundraiser. They want to make at most 60 total garments (hats and scarves). They decide to sell the hats for $10 and scarves for $5. The knitting club is hoping to raise a minimum of $210.
Write the system of inequalities.
x+y<=60
10x+5y>=210
300
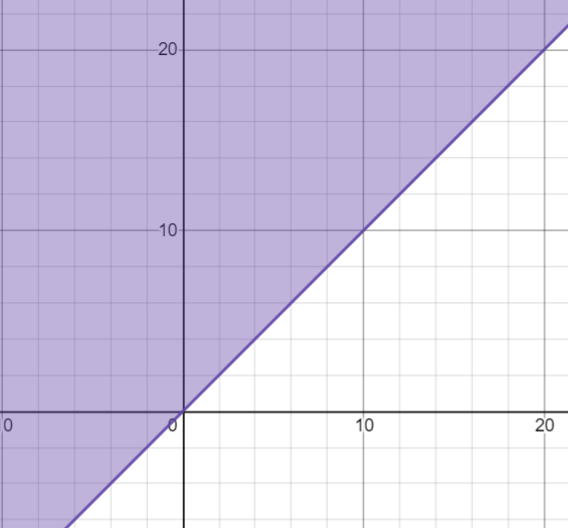
Graph this inequality
y>=x
300
Using the profit line, what is combination that will give the max profit?
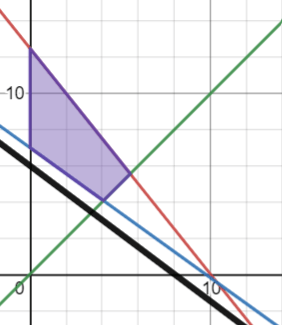
(0, 12.5)
300
Solve the system of equations
3x + 2y = 15
y = x + 5
x = 1 y = 6
solution (1, 6)
300
How do you graph systems of inequalities?
1. Find Intercepts
2. Shade regions based on inequality signs
3. Identify the feasible region/corner points of FR
400
Write the profit expression for the Woos earning $2 for plain dozens and $4 for iced dozens
2P + 4I
400
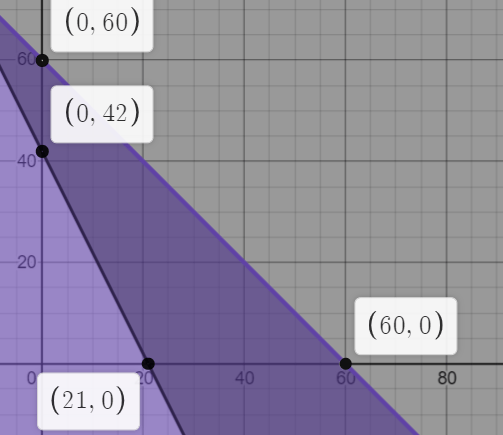
What are the intercepts for this system of inequalities
x+y<=60
10x+5y>=210
(60, 0) and (0, 60)
(21, 0) and (0, 42)
400
What is the max profit if the profit expression is 3000x+4000y
Max Profit $50,000
400
Solve the system:
2x + y = 12
x + 3y = 21
x = 3 y = 6
Solution (3, 6)
400
What the two methods to solve systems of equations algebraically
Substitution and elimination
500
The Rocking Pebbles are playing a concert at Big State University. The auditorium seats 2200 people. The concert manager decides to sell some tickets at $10 each and the rest at $15 each. How many of each kind should the manager sell if he wants ticket sales to total exactly $26,600?
x = $10 tickets
y = $15 tickets
x + y = 2200
10x + 15y = 26,600
500
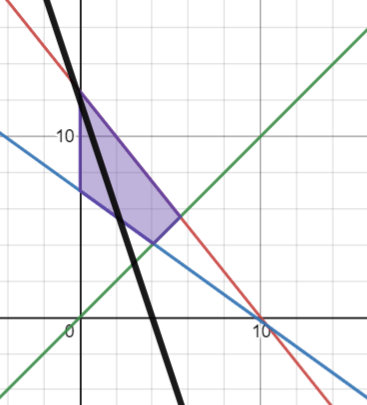
Graph and identify the feasible region
x+y>=60
10x+5y>=210
500
If you change the profit expression to 6000x + 2000y, what would be the max profit?
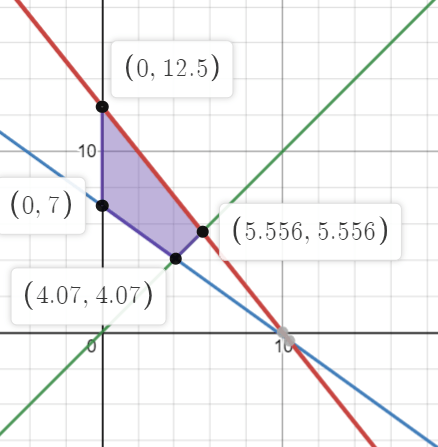
$44,448
500
The Rocking Pebbles are playing a concert at Big State University. The auditorium seats 2200 people. The concert manager decides to sell some tickets at $10 each and the rest at $15 each. How many of each kind should the manager sell if he wants ticket sales to total exactly $26,600?
Manager should sell 1280 tickets for $10 and 920 tickets for $15.
500
What is the line to help find the corner point that will yield the most income?
Max Profit line