Is the set of multiples of 3 between 0 and 40 finite or infinite?
Finite
A = {1, 2, 7, 8, 9}
B = {2, 3, 5, 6, 9}
Find A cap B
A cap B = {2, 9}
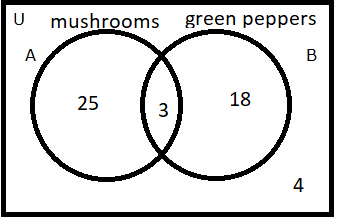
How many people like mushrooms or green peppers?
AcupB ?
46
Write the negation of the statement below.
All Mustangs are Fords
Some Mustangs are not Fords.
What form does this argument follow?
p rightarrow q
p
therefore q
Law of Detachment
(Valid)
A = {January, February, March, ... , December}
What is n(A)?
n(A) = 12
U = {history, math, literature, biology, business, music, criminal justice, art}
A = {math, music, art}
B = {history, literature, criminal justice}
Find BC
BC = {math, biology, business, music, art}
250 students at ACC were surveyed to determine where they studied on campus.
167 studied in the library.
138 studied in the 2nd floor lounge.
75 studied both in the library and the 2nd floor lounge.
How many did not study in the library or the 2nd floor lounge?
20
p: A panther has a long tail.
q: A bobcat can purr.
Write the following symbolic statement in words.
~qwedgep
A bobcat cannot purr and a panther has a long tail.
Is this argument valid or invalid?
p rightarrow q
q
therefore p
Invalid
(Fallacy of the Converse)
Is the following set well-defined or not?
Set A: Top selling Christmas pajamas on Amazon
Not well-defined
[How many top sellers? Top sellers during which time period? etc.]
U = {a, b, c, d, e, ... , x, y, z}
A = {a, b, c, d, e, f, g}
B = {a, e, i, o, u}
C = {a, b, c, p, q, r, x, y}
A cap C
A cap C = {a, b, c}

How many students studied in the library but not in the 2nd floor lounge?
92
Write the inverse of the statement:
If the sun is shining, then we go swimming.
If the sun is not shining, then we do not go swimming.
Is the following argument valid or invalid?
I'm going to buy an SUV or I'm going to buy a truck.
I'm not going to buy an SUV.
Therefore, I'm going to buy a truck.
Valid
(Disjunctive Syllogism)
How many subsets can you make from the set:
{candy cane, elf, snowman, wreath, icicle}
32
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 7, 8, 9}
B = {2, 3, 5, 6, 9}
C = {4, 5, 6, 7}
Find A cup (C cap B)
A cup (C cap B)={1, 2, 5, 6, 7, 8, 9}
Draw a Venn Diagram to represent the following set:
(AcupB)^'

p: A panther has a long tail.
q: A bobcat can purr.
Write the following statement in symbolic form.
It is not true that if a panther has a long tail, then a bobcat can purr.
~(prightarrow q)
Complete the conclusion to build a valid argument.
If John passes the bar exam, then he will practice law.
John will not practice law.
Therefore...
John did not pass the bar exam.
Add element(s) to one or both of the sets to make the statement true.
{cat, dog, horse} subset {cat, dog}
Answers may vary
Add horse and another element to the second set.
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 7, 8, 9}
B = {2, 3, 5, 6, 9}
Find A cup BC
A cup B^C={1, 2,4,7,8,9,10}

Describe the shaded region using
A, B, cup, cap and ^C
as necessary.
(A cap B)^C
Write an equivalent statement using a different symbolic form.
If Joe has an iPad, then Brie has an iPhone.
Answers may vary.
[If Brie doesn't have an iPhone, then Joe doesn't have an iPad. OR Joe doesn't have an iPad or Brie has an iPhone.]
Complete the conclusion to build an invalid argument.
If the car was built in the 1990's, then it has a CD player.
The car was not built in the 1990's.
Therefore... __________________
Therefore, the car does not have a CD player.