Special Segments
Perpendicular and Angle Bisectors
Triangle Centers
Midsegment
Inequalities
100
Which segment is a perpendicular bisector?
∠BAE≅∠CAE; BF≅CF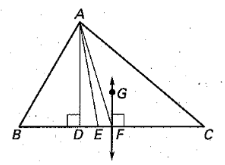
GF
100
Find the measure of SU.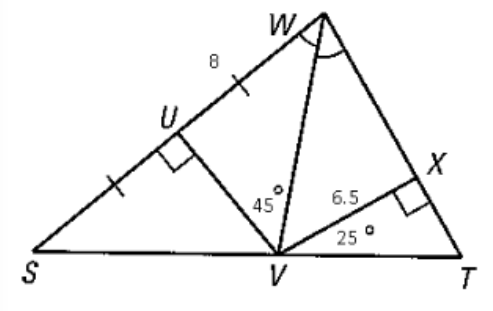
8
100
The point of concurrency of the angle bisectors.
What is the incenter?
100
Use the midsegment theorem to find the value of x.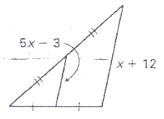
2(5x-3)=x+12
10x-6=x+12
9x=18
x=2
100
Can the following be the side lengths of a triangle?
22, 33, 55
No
22 + 33 is not > 55 (they are equal)
200
Which segment is a median?
∠BAE≅∠CAE; BF≅CF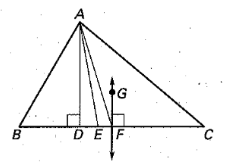
AF
200
Find the m∠UWV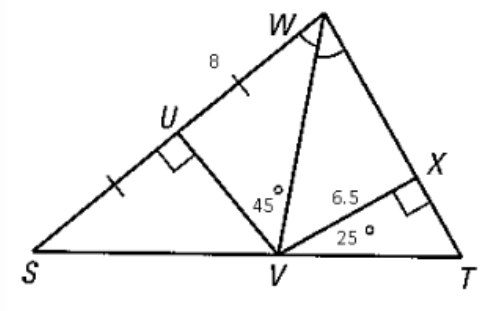
90+45+x=180
135+x=180
x=45
m∠UWV=45
200
The point of concurrency of the altitudes.
What is the orthocenter?
200
Use the midsegment theorem to find the length of the SIDE of the triangle.
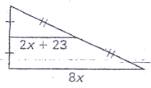
2x+23=1/2(8x)
2x+23=4x
23=4x
11.5=x
8(11.5)=92
200
Use the triangle inequality theorem to order the sides from shortest to longest.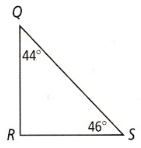 
RS < RQ < QS
300
What triangle center is shown in the following figure?
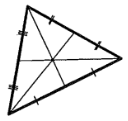
The centroid. Each line segment is a median (midpoint to opposite vertex)
300
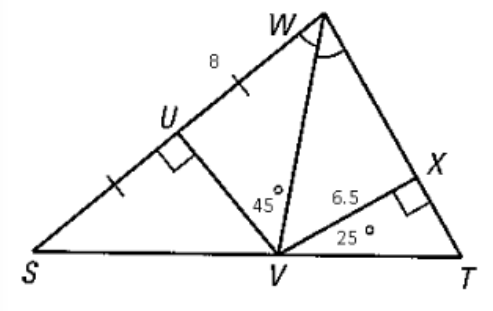Find the m∠WVX
m∠UWV=m∠XWV=45
45+90+x=180
x=45
300
RX is a median of △RST. SX=2x+11 and XT=4x-5. Find ST.
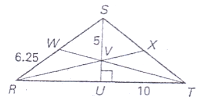
median goes through midpoint (X is a mdpt)
SX=XT
2x+11=4x-5
16=2x
x=8
ST=SX+XT=2(8)+11+4(8)-5 = 54
300
Verify the midsegment theorem by finding the slopes of DE and AC.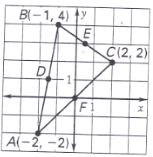
D(-1.5,1) E(0.5, 3)
slope of DE = 2/2 = 1
A( -2,-2) C(2,2)
slope of AC = 4/4 = 1
DE||AC
300
Find the range of possible values for the variable. Express your answer as an inequality.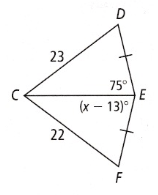
x<88
400
Which segment is an angle bisector?
∠BAE≅∠CAE; BF≅CF
AE
400
Find UV.
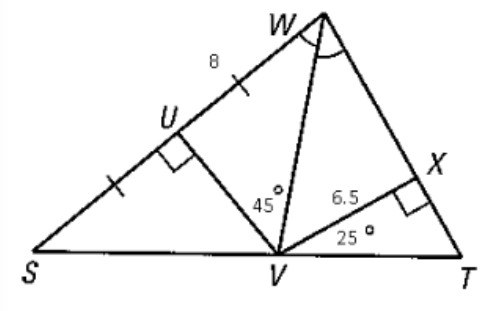
V is on the angle bisector, so it is equidistant to the sides.
Since VX=6.5, UV=6.5
400
The angle bisectors of △ABC meet at point G. Find FG.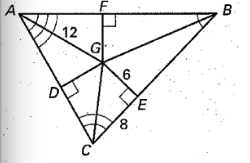
6
400
Verify the midsegment theorem for DE by finding the length of DE and AC.
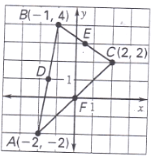
D(-1.5, 1) E(0.5, 3)
DE=√(2²+2²)=√8=2√2
A(-2,-2) C(2,2)
AC=√4²+4²=√32=4√2
AC=2DE
400
Use an inequality to describe a restriction on the value of x.
30<38 so...
3x+2<12x-7
2<9x-7
9<9x
1<x
x>1
500
Based on the markings in the figure, what is AL in △MLT?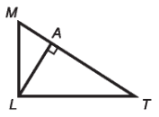
An altitude - perpendicular to a side, but not through the midpoint of the side. Instead it goes through the opposite vertex.
500
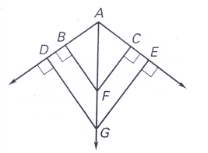If 
G is on the angle bisector of <DAE
500
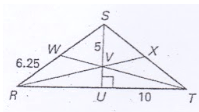V is the centroid of 
5=2/3(SU)
5/(2/3) = 7.5 units
500
In the diagram, EF=5x+6 and AC=3x-2.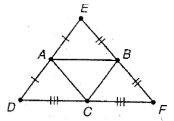
Find EF.
EF=2AC
5x+6 = 2(3x-2)
5x+6 = 6x - 4
10 = x
EF = 56 units
500
Two sides of a triangle are 12 and 17. What are the possible measures of the third side written as a compound inequality?
5<x<29