Write a rational function with an x-intercept at (-1,0), a y-intercept at (0,1/2) and a horizontal asymptote at y=1.
(x+1)/(x+2)
Find the hole of the rational function below.
((x-1)(x-4))/((x-4)(x+2))
(-4, 1/2)
Find the
lim_(x->oo)

0
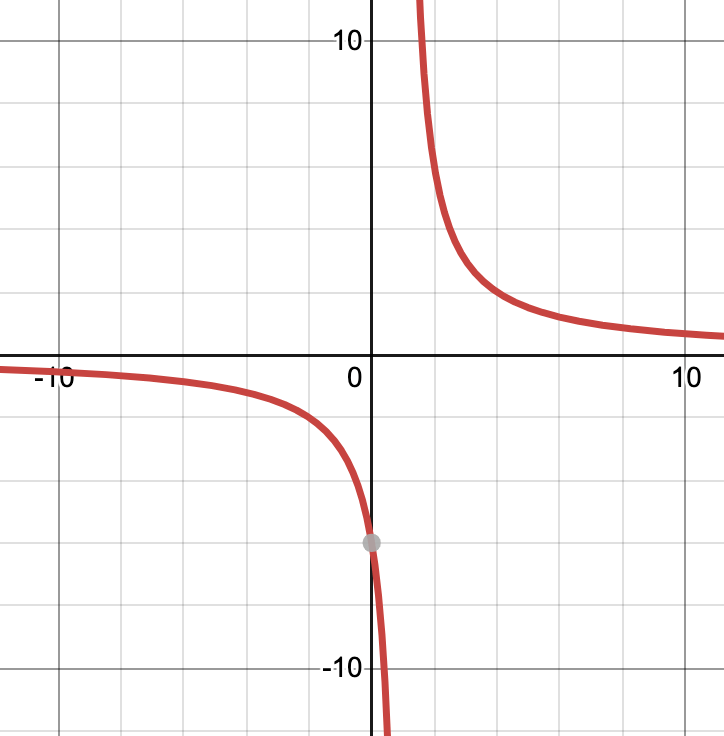
Graph
y=6/(x-1)
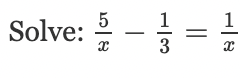
x=12
Write a rational function with a slanted asymptote and a vertical asymptote at x=2
Answers Vary
Top-heavy and (x-2) in denominator
Find the hole of:
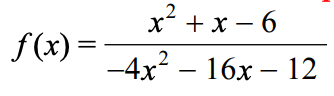
(3,1/2)
Find
Lim_(x->5^+) =
∞
Graph
y= (x+1)/(x-3)
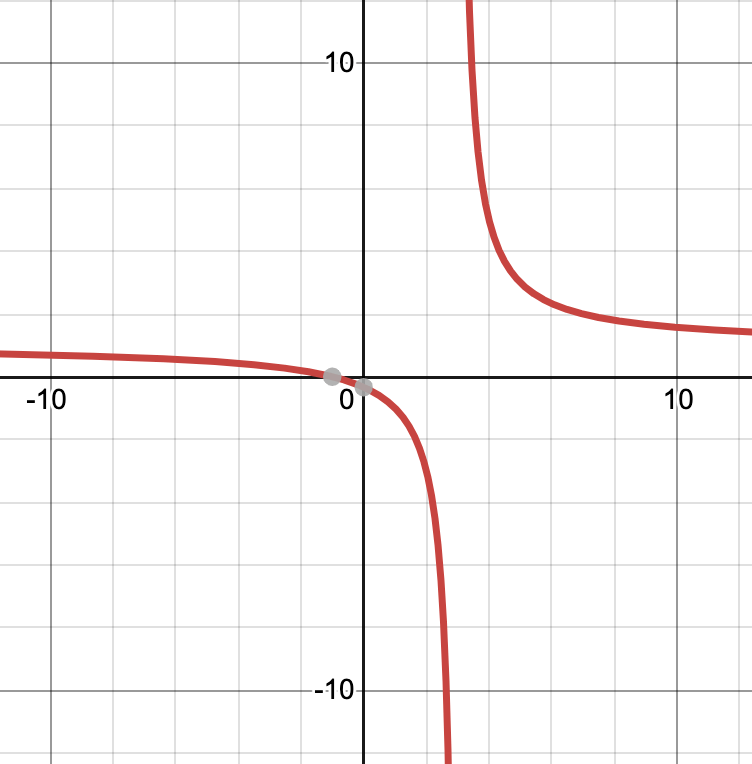
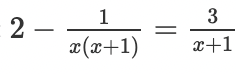
x= -1/2 and 1
Write a rational function with an x-intercept at (4,0) and a y-intercept at (0,2)
Answers Vary
Ex)
(x-4)/(x-2)
Find the hole of:
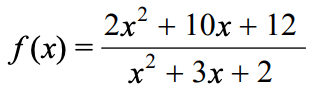
(-2,-2)
Find
Lim_(x->-3^-)=
∞
Graph
y=((x+2)(x-3))/(x+4)

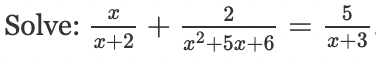
x= 4
(-2 is extraneous)
Write a rational function an x-intercept at -1, a vertical asymptote at x=3 with end behavior
as x-> ∞ , y-> 2
Answers vary
Ex)
(2(x+1))/(x-3)
Graph the function below. Label all asymptotes, intercepts, and holes.
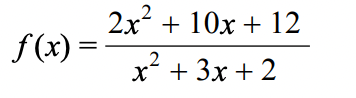
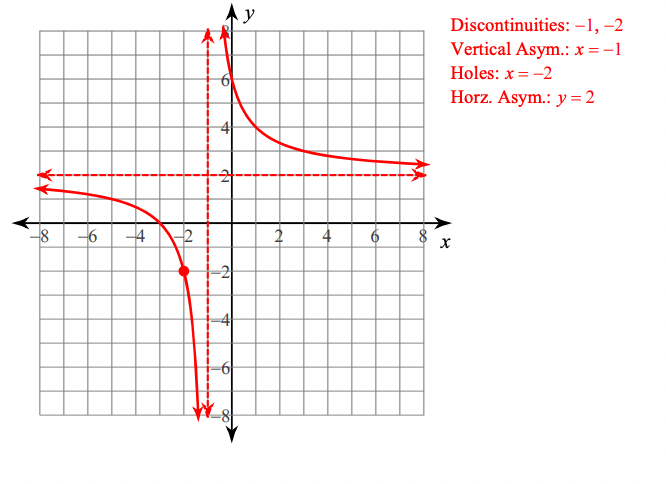
Find
Lim_(x->-∞) (x-2)/(3x+4)
1/3
Graph
y=1/((x-1)^2

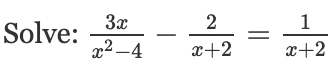
No solution!
Write a rational function that has a hole at (-1,3/4), a vertical asymptote at x=3, and a horizontal asymptote at y=1
y= ((x+1)(x-2))/((x+1)(x-3)
How is a hole created and how do I find it?
A hole is created when a factor is canceled out of the numerator and denominator of a rational function. This creates a "hole" in our graph at an (x,y) point.
Find
Lim_(x->3^-) (x-2)/(x-3)
-∞
What are the steps to graphing a rational function?
YOU MUST BE DETAILED TO GET POINTS (no partial points)
1. Find the x-intercepts by setting the numerator equal to zero
2. Find the y-intercept by setting x equal to zero
3. Find the vertical asymptote by setting the denominator equal to zero
4. Find the horizontal asymptote if the function is bottom-heavy or straight up.
5. Divide to get the slanted asymptote if the function is top-heavy.
6. Graph the asymptotes and intercepts to find the graph pieces.