Solving Systems by Graphing
Solving Systems
Writing Systems
100
How many solutions?
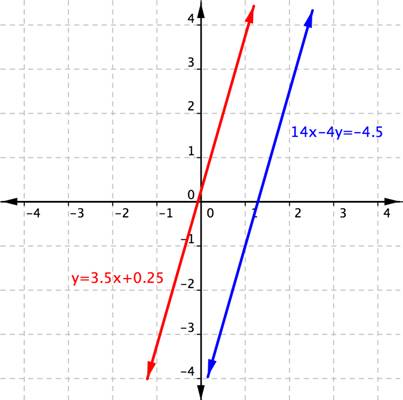
None
100
What is the solution to the system of equations shown.
y = 2x +5
y = x + 4
(-1,3)
100
The state fair is a popular field trip destination. This year the senior class at High School A and the senior class at High School B both planned trips there. The senior class at High School A rented and filled 8 vans and 8 buses with 240 students. High School B rented and filled 4 vans and 1 bus with 54 students. Every van had the same number of students in it as did the buses. Write a system of equations that could be used to find the number of students on a bus.
8v+8b=240
4v+1b=54
200
How many solutions?
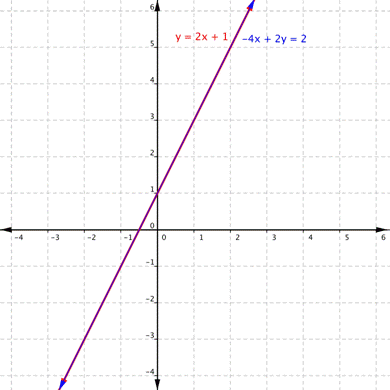
Infinitely many
200
What is the solution to the system of equations shown.
y = 1x - 2
y = 3x - 2
(0,-2)
200
Matt and Ming are selling fruit for a school fundraiser. Customers can buy small boxes of oranges and large boxes of oranges. Matt sold 3 small boxes of oranges and 14 large boxes of oranges for a total of $203. Ming sold 11 small boxes of oranges and 11 large boxes of oranges for a total of $220. Find the cost each of one small box of oranges and one large box of oranges.
3o+14L=$203
11o+11L= $220
300
What is the solution?
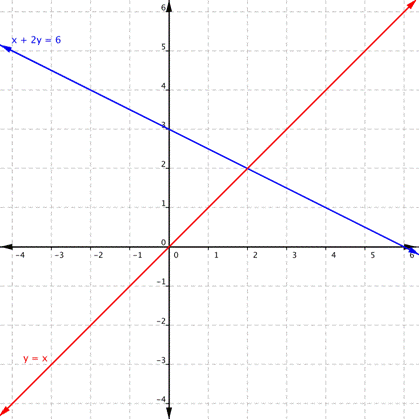
(2,2)
300
What is the solution to the system of equations shown.
y = 1/2x
y = 5x - 30
(6,3)
300
You are running a concession stand at a basketball game. You are selling hot dogs and sodas. Each hot dog costs $1.50 and each soda costs $0.50. At the end of the night you made a total of $78.50. You sold a total of 87 hot dogs and sodas combined. You must report the number of hot dogs sold and the number of sodas sold. Write a system of equations that could determine how many hot dogs and sodas sold.
h+s=87
1.50h+0.50s=78.50
400
Would the following system have one, none, or infinite solutions? Why?
y = -2x + 1
y = -2x + 4
None. The lines are parallel because they have the same slope but different y-intercepts.
400
What is the solution to the system of equations shown.
3x - 2y = 4
y = -1+1x
(2, 1)
400
You and a friend go to Tacos Galore for lunch. You order three soft tacos and three burritos and your total bill is $11.25. Your friend's bill is $10.00 for four soft tacos and two burritos. Write a system of equations that could determine how much a soft taco and burrito cost.
3s+3b=11.25
4s+2b=10
500
What would the graph of this system look like, and how many solutions would there be?
y = -3x - 4
y = -6/2x - 4
Infinitely many solutions. The equations are the same, so the lines would coincide, or be on top of each other.
500
What is the solution to the system of equations shown.
x + 2y = 1
x + y = 2
(3, -1)
500
Kristin spent $131 on shirts. Fancy shirts cost $28 and plain shirts cost $15. If she bought a total of 7 shirts all together, write a system of equations that could determine how much each type of shirt cost.
28F+15p=131
P+F=7