Transformations
Key Features
Conversions
Writing Equations
100
Describe the transformations:
y=-2x^2+5
Reflection in the x-axis
Vertical stretch by a factor of 2
Vertical translation 5 units up
100
What form can we get our y-intercept from?
Standard form, the c value
y=ax^2+bx+c
100
Express in standard form:
y=2(x+3)^2-22
y=2x^2+12x-4
100
Determine the equation in factored form:
y=(x-5)(x+3)
200
Write an equation with the following:
Vertical compression by a factor of 1/4, horizontal translation 2 units right, and a vertical translation 2 units up
y=1/4(x-2)^2+2
200
What is the vertex?
y=2(x-3)^2
(3,0)
200
Express in vertex form:
y=-2(x-1)(x-5)
y=-2(x-3)^2+8
200
The vertex of a parabola is (1,-3), and it has a y-intercept of 1. Write the equation in vertex form.
y=4(x-1)^2-3
300
Describe the transformations:
y=1/5(x-2)^2
Vertical compression by a factor of 1/5, Horizontal translation 2 units right
300
Identify the step pattern and sketch the graph:
y=-3(x-2)^2+4
Step pattern: -3, -9, -15
Graph: 
300
Express in standard form:
y=(x-2)(x+15)
y=x^2+13x-30
300
Determine the equation in vertex form:
y=1/2(x-7)^2+1
400
Write an equation with the following:
Reflection in the x-axis, Horizontal translation 4 units left, Vertical translation 7 units down
y=-(x+4)^2-7
400
What are the zeros?
y=3x^2+15x+18
-3 and -2
400
Express in vertex form:
y=3x^2+6x-6
y=3(x+1)^2-9
400
The parabola has a vertex of (-4,2) and passes through the point (-7,-34). Determine the equation in vertex form.
y=-4(x+4)^2+2
500
Describe the transformations:
y=-4/3(x+2)^2-8
Reflection in the x-axis, Vertical stretch by a factor of 4/3, Horizontal translation 2 units left, Vertical translation 8 units down
500
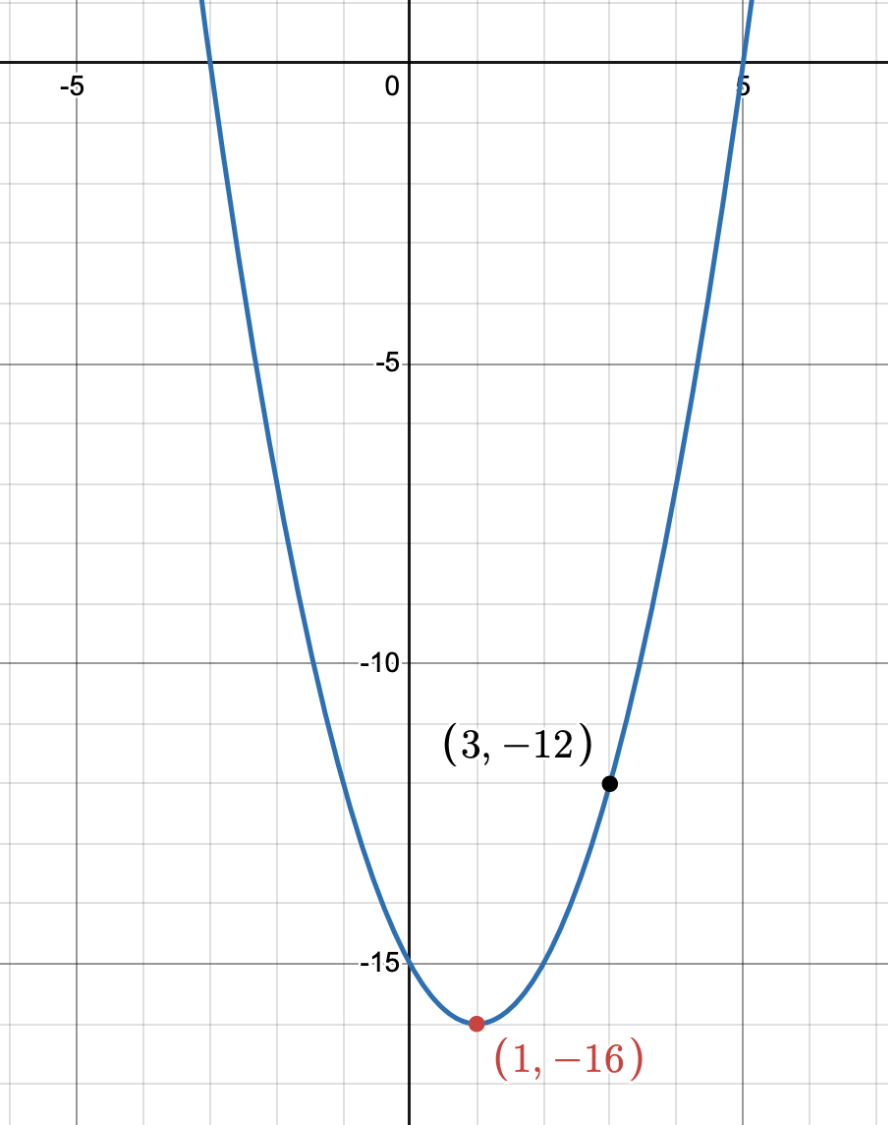
What is the vertex? (hint: x=-b/2a)
y=2x^2+6x-10
(-1.5,-14.5)
500
Express in factored form:
y=-3x^2+12x+15
y=-3(x+1)(x-5)
500
The parabola has zeros at -1 and 4. It's y-intercept is 3. Determine the equation in factored form.
y=-3/4(x-4)(x+1)