Sequences: Recursive
Sequences: Explicit
Summation Notation
Finite Geometric Series
Infinite Geometric Series
100
Determine if the following sequence is Geometric or not:
If it is, determine r. If not, explain why not.
2/7, 3/7, 9/14, 27/28, 81/56
Yes.
r=3/2
100
Consider the following explicit formula for a geometric sequence. Determine the 1st and 10th terms:
a_n=4*(1/2)^(n-1)
a_1=4, a_10=4/2^9
100
Expand the following from sigma notation:
\sum_(k=0)^(2) (k+1)/(k-3)
-1/3 + (-1) + (-3)
100
Determine the sum of the first six terms of the following series:
1/2+1+2+4+. . .
31.5
100
Do the following infinite series converge? Explain why or why not.
(a) \sum_(k=1)^(\infty)2*(-7/4)^(k-1)
(b) \sum_(k=1)^(\infty)2*(2/5)^(k-1)
(c) \sum_(k=1)^(\infty)2*(0.9)^(k-1)
(a) |r| >1 --> diverges
(b) |r|<1 --> converges
(c) |r|<1 --> converges
200
Determine if the following sequence is Geometric or not:
If it is, determine r. If not, explain why not.
6/505-3/101+15/202-75/404+225/808-. . .
Yes.
r=-5/2
200
Write an explicit formula for the following sequence:
8/729-4/243+20/486-100/972+300/1944-. . .
a_n=(8/729)*(-5/3)^(n-1)
200
Expand the following from sigma notation:
\sum_(k=2)^4 (1/k)^(k!)
1/4+1/729+1/4^24
200
Determine the 10th partial sum of the following series:
48-12+3-3/4+. . .
\approx 38.39
200
Determine the sum of the infinite series (if possible):
3/2+9/4+27/16+81/32+. . .
Not possible! |r|=|1.5|>1. The infinite series diverges.
300
Use the following Recursive Formula to find the next THREE terms in the sequence.
a_1=4 , a_n=sqrt(a_(n-1))+2
4 , 4, 4
300
In a certain geometric sequence, the 3rd term is 20 and the 7th term is 1620. Write an explicit formula for this sequence.
a_n=(20/9)*3^(n-1)
300
Evaluate the following sum:
sum_(k=1)^7 (1/2)^(k-1)
\approx 1.98
300
Determine the partial sum of the following series:
\sum_(k=1)^8 2*(5)^(k-1)
195,312
300
Use infinite series to determine what 0.23232323. . . is exactly equal to as a fraction.
23/99
400
Use the following Recursive Formula to find the next THREE terms in the sequence.
a_1=1, a_n=((a_(n-1))!)+(a_(n-1))^2
2, 6, 756
400
A radioactive material is decaying by 75% every hour. If the initial amount of material was 400g, write an explicit formula that demonstrates the grams of radioactive material left after n hours.
a_n=400(1-0.75)^n
400
Rewrite the following series in sigma notation:
2/3+3/4+4/5+. . .
\sum_(k=1)^(\infty) (k+1)/(k+2)
400
Find the sums of the areas of the displayed rectangles to approximate the area under the curve:
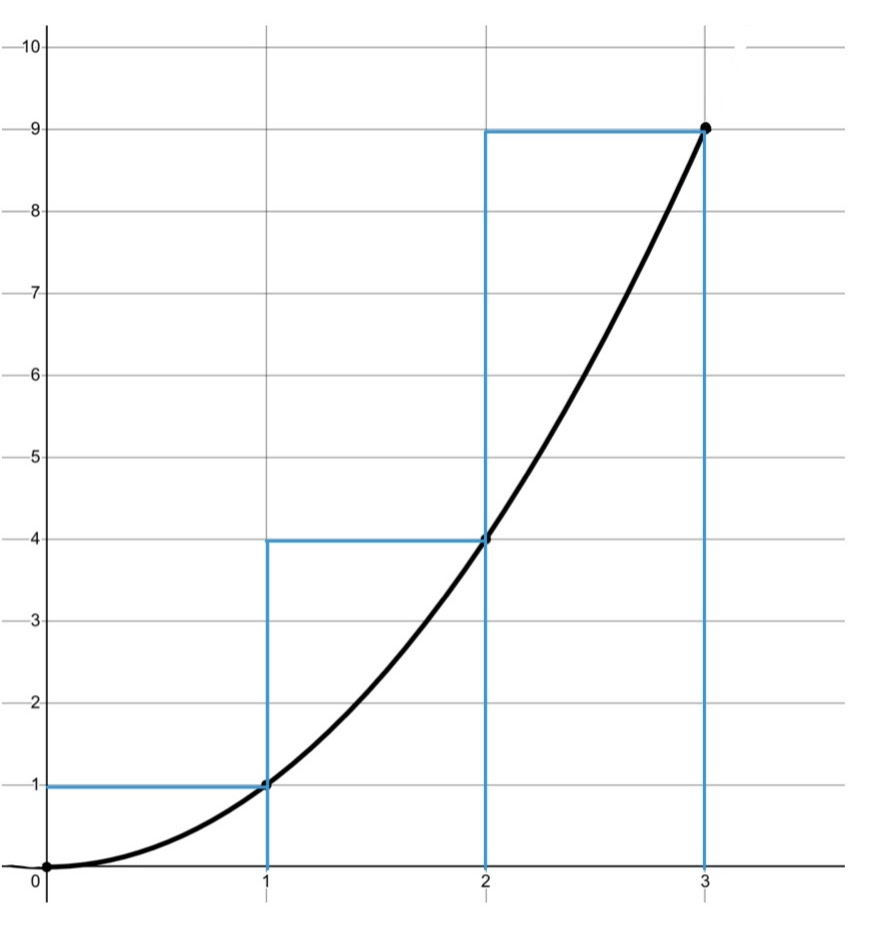
14 units2
400
Determine the sum of the infinite series (if possible):
\sum_(k=1)^(\infty) (8/729)*(-5/3)^(k-1)
Not possible! |r|>1
500
Find the golden ratio by solving for x in the following equation:
x/(1+x)=1/x
(1+sqrt(5))/2
500
Consider the following geometric sequence:
5/pi^6,15/pi^8,45/pi^10,135/pi^12, . . .
At what position (value of
n ) is the term
32805/pi^22?
n=9
500
Rewrite the following series in sigma notation.
1+x^2/(2!)+x^4/(4!)+x^6/(6!)+x^8/(8!)
sum_(k=0)^4 (x^(2k))/((2k)!)
500
The partial sum formula for the Fibonacci Series is shown below. Use this to calculate the sum of the first 10 terms of the Fibonacci sequence.
S_n=F_(n+2)-1
S_10=F_(12)-1=144-1=143
500
Match graphs to sequences.
a_n=(1/4)^n, a_n=(-1/4)^n, a_n=4^n, a_n=(-4)^n
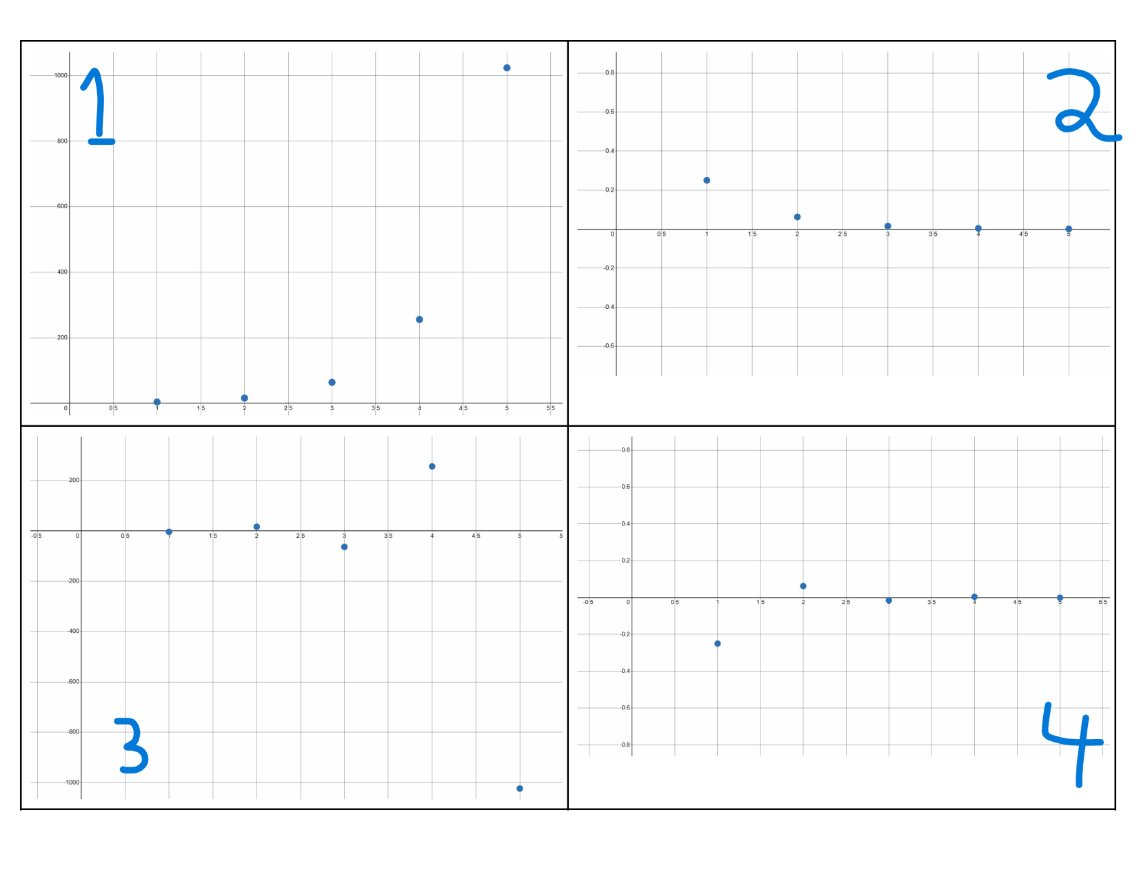
1: 4^n
2: (1/4)^n
3: (-4)^n
4: (-1/4)^n