Systems of Equations
Writing Equations
Reading Graphs
Cost Revenue
100
Describe how you would solve a System of Equations using graphing.
Put both equations into slope-intercept form (y=mx+b), and find the point of intersection on the graph
100
Create an equation (in slope intercept form) to model the situation below.
A diver is 20 feet BELOW the surface of the water. He begins to swim up at ½ foot per second.
y = 1/2x + -20
100
What is the slope of this line?
-1/3
100
In your own words, what is the Cost, Revenue, and Break Even point?
Cost: How much money you loose
Revenue: How much money you gain
Break Even: When cost and revenue are equal
200
Solve the following Systems of Equations using Substitution.
(3,-4)
200
A. For babysitting, Nicole charges a flat fee of $3, plus $5 per hour. Write an equation for the cost, C, after h hours of babysitting.
B. How much money will she make if she babysits 5 hours?
A. C = 5h + 3
B. $28
200
What is the slope?
0
200
What is the equation for Break Even?
R = C
300
Solve the following Systems of Equations using Substitution.
(3,-2)
300
Create two equations (in slope intercept form) that model the situation below for the special offer, and without the special offer. .
The local gym is making a special offer. They usually charge $5 per day to workout at the gym. For the special offer, members can pay an enrollment fee of $10 and then the daily pass will only be $4 per day.
y = 5x
y = 4x+ 10
300
What is the point of intersection of the graphs below?
What does this point represent?
A. (3,2)
B. The point is the solution for the System of Equations
300
Your family decides to rent out a room at your ski cabin. They calculate that it will cost $300 to fix up the room for new guests. Also, it will cost $30 per night to cover food and utilities. Your family decides to charge each family that rents the room $60.
Set up an equation to the model the costs of renting the room.
C = 30x + 300
400
2x - 9y = 14
-6y + 7 = x
(7,0)
400
Jim has to choose between two gym membership plans. Plan A: $50 monthly membership fee and $10 per visit. Plan B: costs $25 monthly one time membership fee and $15 per visit
Which should he choose?
Plan A
400
Lines L and M have the same slope. Using the graph, how many solutions would these two equations have?
0
400
Your family decides to rent out a room at your ski cabin. They calculate that it will cost $300 to fix up the room for new guests. Also, it will cost $30 per night to cover food and utilities. Your family decides to charge each family that rents the room $60.
Set up an equation to model the revenue your family can earn.
R = 60x
500
- 5y + 8x = -18
5y + 2x = 58
(4,10)
500
A. Rufus collected 100 pounds of aluminum cans to recycle. He plans to collect an additional 25 pounds each week. Write and graph the equation for the total pounds, P, of aluminum cans after w weeks.
B. How long will it take Rufus to collect 400 pounds of cans?
A. P= 100 + 25w
B. 12 weeks
500
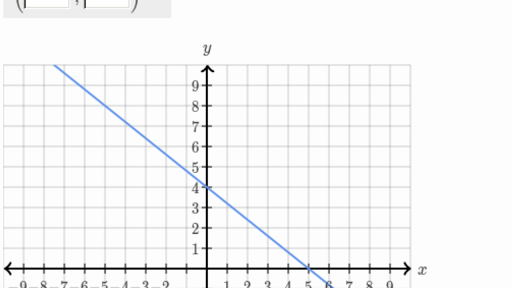
Write the equation of the graph
y = -4/5x + 4
500
Your family decides to rent out a room at your ski cabin. They calculate that it will cost $300 to fix up the room for new guests. Also, it will cost $30 per night to cover food and utilities. Your family decides to charge each family that rents the room $60.
Find the break-even point.
x = 10 days