Describe all transformations from the parent function of g(x)= -2(x+7)2 - 8
- reflection across the x-axis
- Vertical stretch by factor of 2
- Shifted left 7 units
- Shifted down 8 units
The equation h = -16t2 + 20t + 8 models the height of a dirt bikes being launched off a ramp as a function of time. What was the initial height of the bike?
8 feet
Find the average rate of change between from [0,6].
m = -4
y = -2x2 + 8x - 12
Axis of Symmetry:
Vertex:
Domain:
Range:
Increasing:
Decreasing:
AoS: x= -2
Vertex: (-2, -36)
Domain: All real numbers
Range: y < -36
Use the piecewise function below to find f(6)
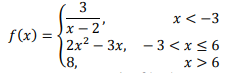
f(6)=54
Write a rule for g(x) described by the transformation of the graph of f(x) and identify the vertex.
" f(x)=x2; vertical compression by factor of 1/4 and a reflecting across the x-axis, followed by a translation 13 units down and 2 units left. "
g(x) = -1/4 (x+2)2 -13
vertex: (-2,-13)
You throw a stone from a height of 48 feet with an upward velocity of 32 feet per second. When does the stone land in the water?
3 seconds
m = 1
f(x) = - 2|x + 3| - 4 and identify the following:
Range: ____________________
Domain: __________________
Vertex: __________________
Range: y < -4
Domain: (-oo, oo)
Vertex: (-3,-4)
-11 and 9
The graph of f(x) = 4(x+2)2 + 3 is reflected over the x-axis, shifted down 2 units and shifted left 4 units. What is the vertex of the new graph?
(-6,-5)
An athlete throws a disc from an initial height of 6 feet and with an initial vertical velocity of 64 ft/sec. What is the max height of the disc?
h(2) = 70 feet
Given the function defined in the table below, find the average rate of change of the function over the interval 6≤x≤60.
m= -5/6
On what interval is the graph of the function p(x) = -3x2 +12x - 4 increasing?
(-oo, 2)
Write a function for the following graph:
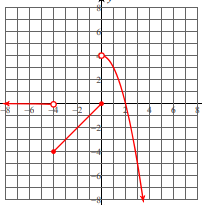
 Write an equation for g(x) and describe the transformations.
Write an equation for g(x) and describe the transformations.
g(x) = (x-3)2 -8
- Shifted right 3 units
- Shifted down 8 units
An underhand volleyball is served with an initial velocity of 24 ft/sec and an initial height of 4 feet. At what time(s) is the ball 12 feet above the ground?
t = 1/2 seconds and 1 second.
The functions f(x) and g(x) are shown below. Order of the functions according to their average rates of change on the interval −3≤x≤1 from least to greatest.
g(x); m=-5
f(x); m= 2
On what interval is the function graphed below decreasing and increasing?
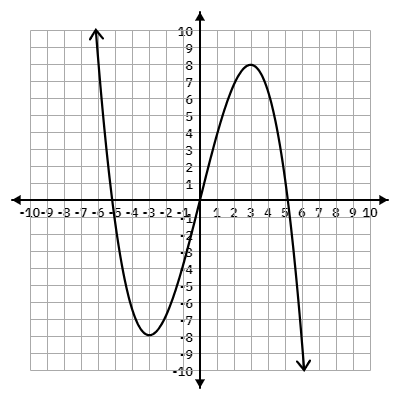
Decreasing:
(-oo,-3)U(3,oo)
Increasing:
(-3,3)
Graph the following and evaluate f(-7).
f(-7) =9
Suppose the function 𝑓(𝑥) = 6𝑥2 + 𝑘𝑥 +30 is a translation up 6 units and left 2 units of the function 𝑔(𝑥) = 6x2. Use the translations to write a vertex form equation and convert that equation to standard form to determine the value of k.
k=24
Fred and Alex ran up the stairs. Fred jumped down from a height of 4 feet at an initial velocity of 12 ft/sec. Alex jumped down at the same time with an initial velocity that was 8 ft/sec faster and from a height 2 feet higher than Fred's. Who landed on the ground first?
Fred: 1 second, Alex: 1.5 seconds.
Fred landed first.
The functions g(x) and h(x) are shown below. Order the functions according to their average rates of change on the interval 2< x < 3 from least to greatest.
g(x); m=-10 and h(x); m=-6
g(x),h(x)
g(x) = -4x2 + 2x - 1 state the key features:
1. y-Intercept
2. Vertex
3. Axis of Symmetry
4. Domain
5. Range
6. Increasing Interval
7. Decreasing Interval
1. y-Intercept: (0,-1)
2. Vertex: (1/4, -3/4)
3. Axis of Symmetry: x=1/4
4. Domain: All real numbers
5. Range: y < -3/4
6. Increasing Interval (-oo, 1/4)
7. Decreasing Interval (1/4, oo)
Write a function and evaluate f(-3) and f(x)=1.
f(-3) = 2
f(x) = 1, x=-4,-2,3