Part 2
What would you change the base to?
a) 8x-1 = 2x+2
b) 6x+7 = 36
c) 84x = 4x-2
d) 53x+1 = 25x+1
e) 27 = 99x
f) 16x = 4x+1
a) 2
b) 6
c) 2
d) 5
e) 3
f) 4
Could this situation be modeled using an arithmetic or geometric sequence?
A retail store just started a big sale. One day after the sale begins, the store has 43 customers. For every subsequent day, the number of customers quadruples from the previous day.
Geometric
Could this situation be modeled using an arithmetic or geometric sequence?
Biologists are studying the population of water lilies in a pond. One month after beginning the study, there are 23 lilies in the pond. For every subsequent month, the population has 20 more lilies from the previous month.
Arithmetic
Jimmy opened a bank account earning annual compound interest. The balance in the account after x years can be modeled by g(x) = 675(1.035)x.
Which statement is the best interpretation of one of the values in this function?
a) The balance of the account decreases at a rate of 96.5% each year.
b) The balance in the account increases at a rate of 3.5% each year.
c) The initial balance of the account was $1035.
d) The balance in the account at the end of the year is $675.
b) The balance in the account increases at a rate of 3.5% each year.
Jenny opened a bank account earning annual compound interest. The balance in the account after x years can be modeled by g(x) = 1500(1.015)x.
Which statement is the best interpretation of one of the values in this function?
a) The balance of the account decreases at a rate of 98.5% each year.
b) The balance in the account increases at a rate of 1.5% each year.
c) The initial balance of the account was $1015.
d) The balance in the account at the end of the year is $1500.
b) The balance in the account increases at a rate of 1.5% each year.
Solve.
53x+1 = 25x+1
x=1
Could this situation be modeled using an arithmetic or geometric sequence?
A carnival game operator starts off the day with 140 prizes. Each person who wins at this game earns 4 prizes.
Arithmetic
Could this situation be modeled using an arithmetic or geometric sequence?
A town has a growing population. After one year of monitoring, the population is 2704 people. Each year afterwards, the population increases by 5%.
Geometric
Jenny invested $300. She earned a compound interest of 3% per year on the initial investment. If no money was added or removed from the investment, what was the amount of interest Jenny received at the end of three years?
$27.82
Jimmy invested $500. He earned a compound interest of 5% per year on the initial investment. If no money was added or removed from the investment, what was the amount of interest Jimmy received at the end of five years?
$138.14
Solve.
1442x+1 = 125x-1
x=3
Use the graph below to answer the following questions.
Find each of the terms defined below:
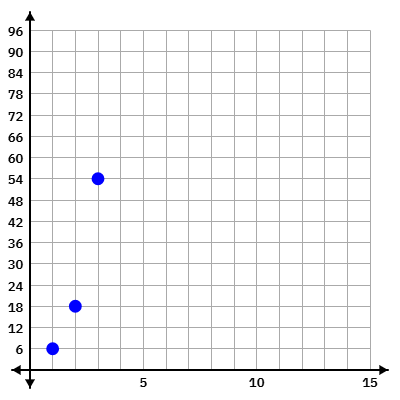
a8 = a12 =
a8 = 13122
a12 = 1062882
Use the graph below to answer the following questions.
Find each of the terms defined below:
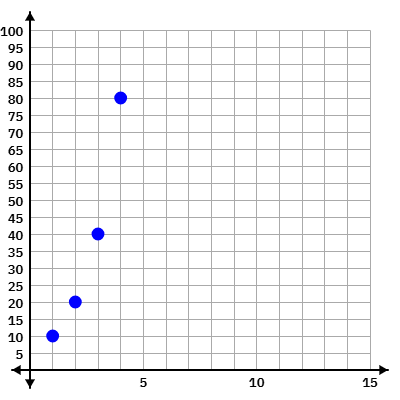
a7 = a11 =
a7 = 640
a11 = 10240
Jimmy keeps $600 in a piggybank at home. He also deposits $900 in a savings account that earns 2.3% compound interest. Which function models the total amount of money Jimmy has over time, t?
a) f(t) = 600(1.023)t
b) f(t) = 900(1.023)t + 600
c) f(t) = 900(1.023)t + 600t
d) f(t) = 900(300.023)t
b) f(t) = 900(1.023)t + 600
Jenny keeps $750 in a safe at home. She also deposits $1100 in a savings account that earns 1.8% compound interest. Which function models the total amount of money Jenny has over time, t?
a) f(t) = 750(1.018)t
b) f(t) = 1100(1.018)t + 750
c) f(t) = 1100(1.018)t + 750t
d) f(t) = 1100(750.018)t
b) f(t) = 1100(1.018)t + 750
What would be the next step in solving exponential equation?
Step 1: 16x+1 = 44x+1
Step 2: 42(x+1) = 44x+1
Step 3: ??
Cancel the bases and distribute.
Use the given information to write the Explicit Formula for each sequence.
Sequence A:
a1 = 11, Common Ratio: r = 3
an =
Sequence B:
a1 = 9, Common Difference: d = 2
an =
Which of the sequences has the greater 10th term?
11(3)n-1
9+2(n-1)
Sequence A
Use the given information to write the Explicit Formula for each sequence.
Sequence A:
a1 = 15, Common Ratio: r = 4
an =
Sequence B:
a1 = 8, Common Difference: d = 5
an =
Which of the sequences has the greater 12th term?
15(4)n-1
8+5(n-1)
Sequence A
Jimmy's character in a video game gains 3 points the first time he collects a coin, and gains 1 point for each coin he collects after that.
a) What type of sequence does this situation model?
b) Write the Explicit Formula that correctly models this situation: an =
Jenny's character in a different video game also gains 3 points the first time she collects a coin, then her points double for each coin she collects after that.
c) What type of sequence does this situation model?
d) Write the Explicit Formula that correctly models this situation: an =
e) If both characters collect the same number of coins at the same time, who will earn 100 points first?
a) Arithmetic
b) 3+1(n-1)
c) Geometric
d) 3(2)n-1
e) Jenny
Jenny is training for a marathon. On her first day of training, she runs 4 miles. Everyday after that, she doubles the amount of miles she runs.
a) What type of sequence does this situation model?
b) Write the Explicit Formula that correctly models this situation: an =
Jimmy is also training for a marathon and runs 4 miles on his first day of training. Everyday after that, he runs 3 more miles than the day before.
c) What type of sequence does this situation model?
d) Write the Explicit Formula that correctly models this situation: an =
e) If both Jenny and Jimmy continue to run at their current pace, who will reach the 26.2 mile goal quicker?
a) Geometric
b) 4(2)n-1
c) Arithmetic
d) 4+3(n-1)
e) Jenny
Jimmy solved the following equation but he made a mistake. In what step did he make the error?
Solve the equation: Step 1: 62(2x) = 44(2x-1)
362x = 2562x-1 Step 2: 2(2x) = 4(2x-1)
Step 3: 4x = 8x-4
Step 4: -4x = -4
Step 5: x = 1
Step 1
A geometric sequence is defined by the explicit formula shown.
an = -5(3)n-1
What are the first three terms of this sequence?
a1 =
a2 =
a3 =
a1 = -5
a2 = -15
a3 = -45
A geometric sequence is defined by the explicit formula shown.
an = 2(5)n-1
What are the first three terms of this sequence?
a1 =
a2 =
a3 =
a1 = 2
a2 = 10
a3 = 50
Jimmy and Jenny each opened a savings account with a deposit of $200.
- Jimmy earned 3.5% simple interest per year.
- Jenny earned 3.5% compound interest per year.
- Neither of them made additional deposits or withdrawals.
How much more money did Jenny have in her account than Jimmy after 7 years?
$5.46
Jimmy and Jenny each opened a savings account with a deposit of $150.
- Jenny earned 1.5% simple interest per year.
- Jimmy earned 1.5% compound interest per year.
- Neither of them made additional deposits or withdrawals.
How much more money did Jenny have in her account than Jimmy after 10 years?
$1.58