Classify each type of transformation (translation, reflection, or dilation):
a. (x, y) -> (x+1, y-1)
b. (x, y) -> (2x, 2y)
c. (x, y) -> (-x, y)
a. Translation
b. Dilation
C. Reflection
A circle has center (9, -6) and radius 7 units. Write an equation that represents the circle.
(x-9)^2+(y+6)^2=7^2
What is the first step to completing the square to find the radius and center of the circle given by the equation x^2+y^2+8x-6y+21=0 ?
Rearrange the equation so that like terms are together and the constant (21) is on the right side
x^2+8x+y^2-6y=-21
The parabola has a focus at (6, 2). Its directrix is the line y=1. Write an equation to represent the parabola.
(x-6)^2+(y-2)^2=(y-1)^2
Use the Pythagorean Theorem to find the length of side AD of the square.
3^2+4^2=c^2
9+16=c^2
25=c^2
c=sqrt25=5
Describe the transformation used to take figure F to figure G
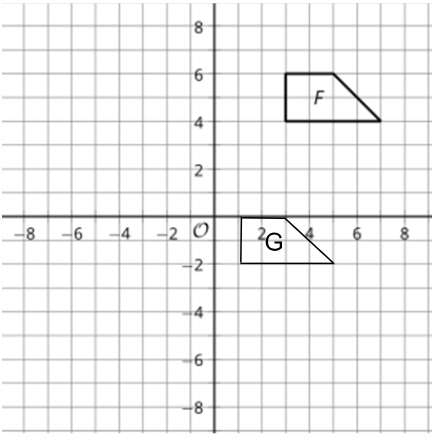
Translation 6 units down and 2 units left
Describe the process to test if a point is on a circle.
Plug the x and y values of the point in for x and y in the equation. If you end up with the same number on both sides of the equation, the point is on the circle.
Find the missing numbers to complete the square: x^2+8x+[ ]+y^2-6y+[ ] =-21+[ ]+[ ]
x^2+8x+16+y^2-6y+9 =-21+16+9
The point (9, 6) is on the parabola. Find the distance between this point and the focus.
5 (same as the distance to the directrix)
What needs to be true for a quadrilateral to be a square?
What types of transformations result in figures that are congruent to the original?
Rigid Transformations (translations, reflections, and rotations)
Use your equation from #1 to identify if point (9, 1) lies on the circle.
(9-9)^2+(1+6)^2=7^2
0+7^2=7^2
49=49
What should you do after finding your missing numbers?
Add up the numbers on the right side
OR
Rewrite the equation using squared binomials
Write an equation for a line with slope 3/7 passing through point (7, -1).
y+1=3/7(x-7)
How do you find the perimeter of a square?
Add up all the side lengths
What types of transformations result in figures that are similar to the original?
Dilations
Find the center and radius of the circle:
(x-6)^2+(y+4)^2=36
Center: (6, -4) Radius: 6
Rewrite the equation x^2+8x+16+y^2-6y+9=4 using squared binomials.
(x+4)^2+(y-3)^2=2^2
Write an equation for a line that passes through point
(6, 2) that is parallel to
y-3=2(x+1) .
y-2=2(x-6)
How do you find the area of a square?
length x width
OR
side^2
Describe how you would perform the transformation (x, y)-> (x-4, y+3)
Move each point on the shape 4 units to the left and 3 units up. Connect these new dots to form the new shape.
Rewrite x^2+8x+16+y^2-14x+49=81 using squared binomials.
(x+4)^2+(y-7)^2=9^2
What is the radius and center of the equation from #4?
Center: (-4, 3) Radius: 2
Line p is represented by the equation y-1=1/2(x+2) . Select all equations that represent lines perpendicular to line p.
A. y=-1/2x+4
B. y=2/1x+4
C. y=-2/1x+4
D. y=-4/2x+4
C, D
How would you find the slope of a line that passes through points (3, 6) and (7, 10)?
(rise)/(run)=(y_2 -y_1)/(x_2-x_1)=(10-6)/(7-3)=4/4=1