Solve for the area of the circle shown.
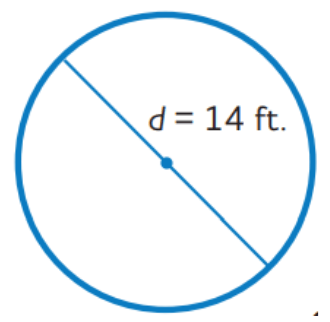
153.86 ft squared
Solve for the measure of angle b.
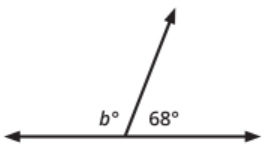
b = 112 degrees
Will the following side lengths make a triangle? Explain your answer.
3 feet, 4 feet, 8 feet
No, because when you add the two smallest sides together they are less than the biggest side (3 + 4 = 7, and 7 is less than 8)
Solve for the measure of angle a:
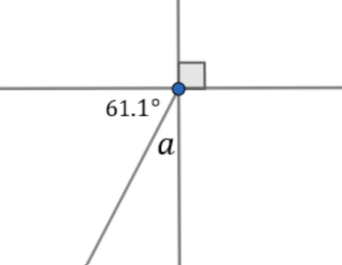
28.9 degrees
Can the following angle measurements make a triangle? Explain why or why not.
12 degrees, 85 degrees, 20 degrees
No, because the sum of the angles is not 180 degrees.
Solve for the circumference of the circle shown.
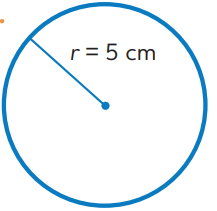
31.4 ft
Solve for the measure of angle y.
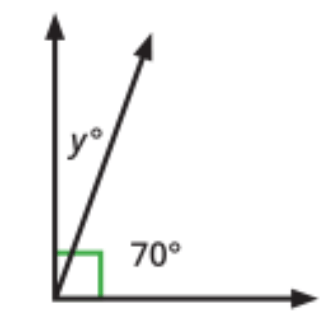
y = 20 degrees
Ms. Latouche drew a triangle. What is the measure of the last angle?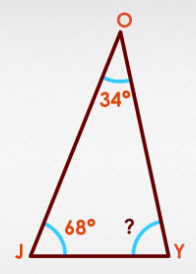
78 degrees
Are these triangles unique or identical?
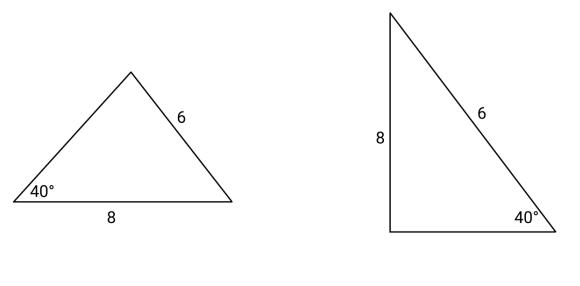
No, because the position of the side lengths are different on the two triangles.
Describe the angle relationship between a and b.
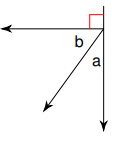
Ms. Giles has a circular rug. From the center to the edge of the rug is 4 feet. What is the distance around the edge of her rug?
25.12 feet
If the measure of angle 1 is 25 degrees, determine the measure of angles 2 and 3.
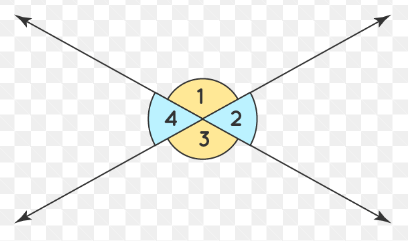
angle 3 = 25 degrees
Will the following side lengths make a triangle?
1 cm, 5 cm, 5 cm
Yes!
A semicircle with a diameter of 6cm is on top of a trapezoid. Solve for the area of the figure shown.
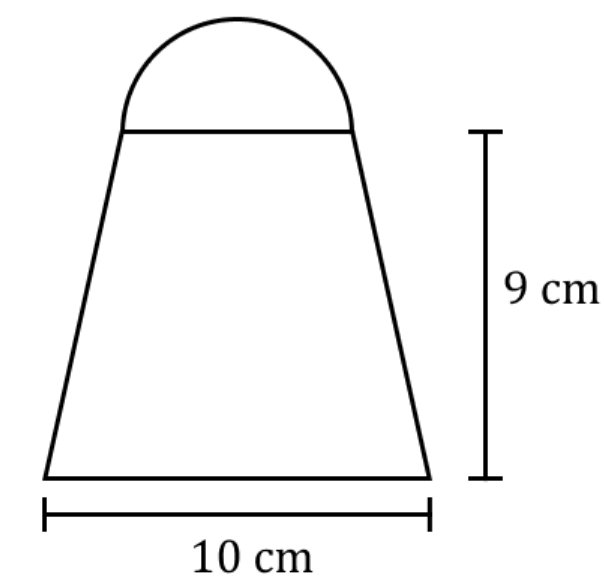
86.13 cm squared
A circle has a radius of 3 meters. Solve for the circumference.
18.84 meters
A circle has a circumference of 25.12 inches. What is the radius of the circle?
4 inches
Determine the measure of angles x, y, and z.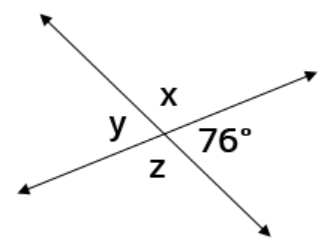
x = 104 degrees
y = 76 degrees
z = 104 degrees
Two of the interior angles of a triangle are 30 degrees and 40 degrees. What is the measure of the last angle?
110 degrees
Solve for x
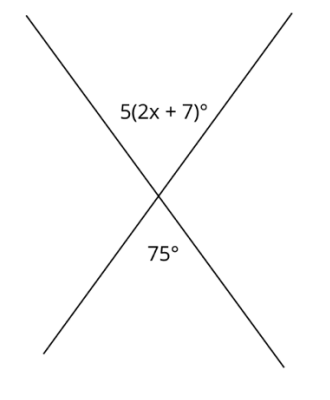
x = 4
The circumference of a circle is 51.81cm. What is the radius of the circle?
8.25 cm
Ms. Long has a circular clock that she wants to hang on her wall. The distance from one end to the other is 9 inches. How much space will the clock take up on her wall?
63.585 inches squared
Solve for the measure of the angles shown.
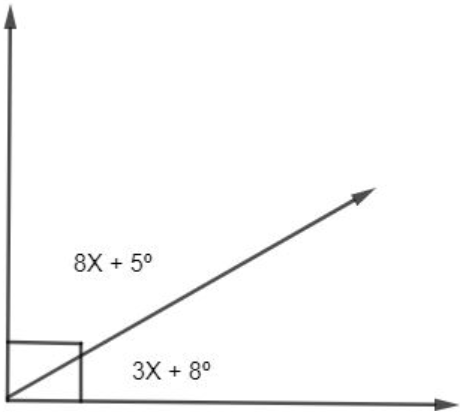
x = 7
Angle 1 = 61 degrees
Angle 2 = 29 degrees
A triangle has one angle that is 20 degrees, one side length that is 4 meters, and another side length that is 6 meters long. Is it possible to make two DIFFERENT triangles with these measurements, or is this a unique triangle? Draw the triangles to prove your answer.
Possible to make different triangles depending on the position of angles nad side lengths.
Solve for the measure of angle EFD
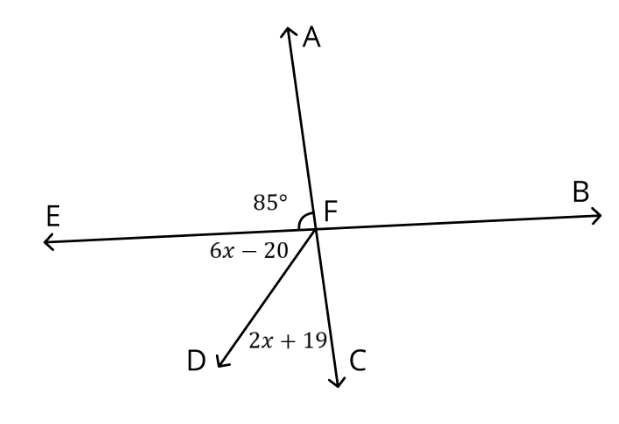
52 degrees
Solve for x, and the measure of the angle indicated.
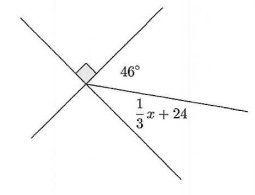
x = 60
Angle = 44 degrees