Graphs
Theorems
Complex #
Rational Functions
Partial Fractions
100
What are the end behaviors in limits form?
lim f(x) = -∞ lim f(x) = ∞
x → -∞ x → ∞
100
Using the factor theorem is x-3 a factor of x3-4x2+2x-5
It is not a factor because when you plug in 3 it doesn't equal 0
100
f(x)
Degree = 4
Zeros = 3-6i, 9+12i
Find the remaining zeros
3+6i, 9-12i
100
List the horizontal asymptote(s).
y=3/[(x-2)(x-3)]
y = 0
100
Write the partial fractions decomposition of
x/(x2-5x+6)
3/(x-3) + -2/(x-2)
200
What are the local maximums and local minimums?
local max: 2, 1
local min: -3, -1
200
Using Descartes' Rule of Signs find how many possible positive and negative zeros the function f(x)=x4+3x3-2x2-x-12
1 possible positive zero, and 3 or 1 possible negative zeros
200
Find all the zeros of
x4-84
± 3i, ± 3
200
Solve for the y-intercept
y = 3/[(x-2)(x+3)]
(0, 1/2)
200
Write the partial fractions decomposition of
(3x-2)/(x2-6x+8)
5/(x-4) - 2/(x-2)
300
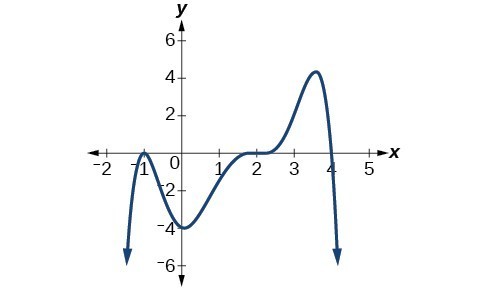
What is the concavity from -.5 to .5?
Concave up
300
List the potential rational zeros of f(x)=4x3-2x2+5x-12
±1, ±1/2, ±1/3, ±1/4, ±1/6, ±1/12, ±2, ±2/3, ±4, ±4/3, ±2/3
300
i4-i86-i66+i45
3+i
300
Find the domain, range, hole, and x-intercept of the following function (interval notation).
y = [(3x-1)(x-2)]/(x-2)
D: (-∞, 2) U (2, ∞)
R: (-∞, ∞)
Hole: (2, 5)
X-Int: (1/3, 0)
300
Write the partial fractions decomposition of
(x+2)/(x3-2x2+x)
2/x + -2/(x-1) + 3/(x-1)2
400
Where is the graph increasing and decreasing? (In interval notation)
Increasing: (-∞ , -1) U (0, 2) U (2, 3.5)
Decreasing: (1, 0) U (3.5, ∞ )
400
Using the Intermediate Value Theorem state if there is a zero between 0 and 5 on the function f(x)=4x4-5x3+3x2-7x-16
Yes there is a zero
400
Find the zeros of :
f(x) = x4+7x2-144
± 3, ± 4i
400
Solve the following inequality and express your answer in interval notation.
(4x+2)/(x-1) ≤ 1
[-1, 1)
400
Write the partial fractions decomposition of
(3x+10)/(20x2-x-12)
-1/(4x+3) + 2/(5x-4)
500
-6x19+13x13-240x2+100x7+97x
Find the symmetry: odd, even, neither?
Neither
500
Using the Rational Zeros Theorem list the potential zeros of f(x)=3x4-2x3+4x2-8x-32
±1, ±1/2, ±1/3, ±1/4, ±1/8, ±1/16, ±1/32, ±3, ±3/2, ±3/4, ±3/8, ±3/16, ±3/32
500
f(x) = x3-5x2+8x-6
Zero = 1-i
Find the remaining zeros of f(x)
1+i,3
500
Solve the following inequality and express your answer in interval notation.
(3x-4)/(x2+4x+1) < 0
(-∞, -√3 -2) U (√3 -2, 4/3)
500
Write the partial fractions decomposition of
(x2-29x+5)/[(x-4)2(x2+3)]
1/(x-4) - 4/(x-4)2 + (-x+2)/(x2+3)