Significance Testing
Basics
Basics
Two-Sided
Testing
Testing
Small
Samples
Samples
Power and
Type I & II Errors
Type I & II Errors
100
Two years ago 72% of households in a certain county regularly participated in recycling household waste. The county government wishes to investigate whether that proportion has increased after an intensive campaign promoting recycling. In a survey of 900 households, 674 regularly participate in recycling.
Write the hypotheses the government should test. Make sure to define your parameter.
Ho: p = 0.72
Ha: p > 0.72
where p = the proportion of households in the county that recycle household waste.
100
The average household size in a certain region several years ago was 3.14 persons. A sociologist wishes to test, at the 5% level of significance, whether it is different now. In a random sample of 75 households, the average size was 2.98 persons, with sample standard deviation 0.82 person.
Determine the P-value.
t=frac{\bar{x}-\mu_o}{s_x"/"\sqrt(n)}=frac{2.98-3.14}{0.82"/"\sqrt(75)}=-1.6898
df = 75-1 = 74
P-value = 2(0.0476) = 0.0953
100
The histogram below shows the ages of 20 houses on a particular street. What can you say about the distribution of this sample?
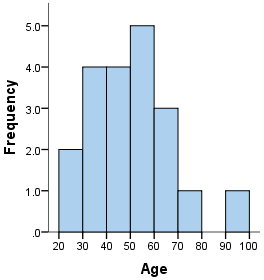
This distribution does not show strong skew or outliers, so we are able to proceed.
100
What are the two changes a researcher can make to their hypothesis test to increase the power of the test?
1) Increase the sample size
2) Increase the significance level (alpha).
200
Two years ago 72% of households in a certain county regularly participated in recycling household waste. The county government wishes to investigate whether that proportion has increased after an intensive campaign promoting recycling. In a survey of 900 random households, 674 regularly participate in recycling.
Check the conditions for performing the hypothesis test.
- Sample is randomly selected households
- 900 households is less than 10% of all households in a county
- n(po) = (900)(0.72) = 648 > 10
n(1-po) = (900)(0.28) = 252 > 10
The large counts condition is met so the sampling distribution is approximately Normal.
200
The average household size in a certain region several years ago was 3.14 persons. A sociologist wishes to test, at the 5% level of significance, whether it is different now. In a random sample of 75 households, the average size was 2.98 persons, with sample standard deviation 0.82 person. This produces a P-value of 0.0953.
What conclusion would you make?
Since the P-value of 0.0953 is greater than alpha = 0.05, we fail to reject Ho. There is not convincing evidence that the average household size is different from 3.14 people.
200
If the sample size is not big enough, what does that mean about the shape of the sampling distribution?
The sampling distribution (and sample distribution) will have the same shape as the population distribution.
200
The average number of days to complete recovery from a particular type of knee operation is 123.7 days. From his experience, a physician suspects that use of a topical pain medication might be lengthening the recovery time.
The power of a test to detect mu = 135 days with a significance level of alpha = 0.05 is 0.801. What are the probabilities of a Type I and Type II error in this scenario?
P(Type I) = alpha = 0.05
P(Type II) = 1 - Power = 1 - 0.801 = 0.199
300
Two years ago 72% of households in a certain county regularly participated in recycling household waste. The county government wishes to investigate whether that proportion has increased after an intensive campaign promoting recycling. In a survey of 900 random households, 674 regularly participate in recycling.
Determine the P-value for this test.
z=frac{hat{p}-p_0}{sqrt(frac{p_0(1-p_o)}{n})}=frac{0.749-0.72}{sqrt(frac{0.72(1-0.72)}{900})}=1.9376
P-value = 0.0263
300
The average household size in a certain region several years ago was 3.14 persons. A sociologist wishes to test, at the 5% level of significance, whether it is different now. In a random sample of 75 households, the average size was 2.98 persons, with sample standard deviation 0.82 person. This produces a P-value of 0.0953.
Interpret this P-value.
If the household size in this region is 3.14 people, then there is a probability of 0.0953 that we would get a sample household size as far away from 3.14 as 2.98 or farther in a sample of 75 households by chance.
300
Determine the mean and sample standard deviation for the following sample:
21, 23, 21, 18, 21, 19, 16, 23, 23, 22, 19, 25
bar{x}=20.917
s_x=2.539
300
The average number of days to complete recovery from a particular type of knee operation is 123.7 days. From his experience, a physician suspects that use of a topical pain medication might be lengthening the recovery time.
The power of a test to detect mu = 135 days with a significance level of alpha = 0.05 is 0.801. Interpret this value.
If the true mean recovery time is 135 days, there is a probability of 0.801 that they will find convincing evidence that the mean recovery time is greater than 123.7 days.
400
Two years ago 72% of households in a certain county regularly participated in recycling household waste. The county government wishes to investigate whether that proportion has increased after an intensive campaign promoting recycling. In a survey of 900 random households, 674 regularly participate in recycling.
Conducting the hypothesis test yields a P-value of 0.0263. Interpret this P-value.
If the true proportion of households that recycle in the county is 72%, then there is a probability of 0.0263 that we find a sample proportion of 74.9% or greater in a random sample of 900 households by chance.
400
The average household size in a certain region several years ago was 3.14 persons. A sociologist wishes to test, at the 5% level of significance, whether it is different now. In a random sample of 75 households, the average size was 2.98 persons, with sample standard deviation 0.82 person. This produces a P-value of 0.0953.
Would you expect 3.14 to be in the confidence interval for the average household size based on this sample? Explain your reasoning.
Yes. We failed to reject Ho, so we are considering po = 3.14 as a plausible value for mu = the average household size. Therefore we would expect 3.14 to be within our 95% CI of plausible values for mu.
400
Create a graph of the following data set and assess the suitability of this data for a hypothesis test:
21, 23, 21, 18, 21, 19, 16, 23, 23, 22, 19, 25
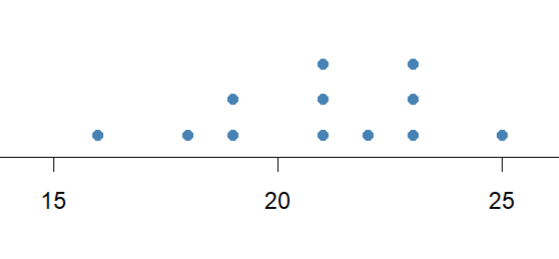
The data does not show strong skewness or outliers. It is suitable to use for a hypothesis test.
400
The average number of days to complete recovery from a particular type of knee operation is 123.7 days. From his experience, a physician suspects that use of a topical pain medication might be lengthening the recovery time.
The power of a test to detect mu = 135 days with a significance level of alpha = 0.05 is 0.801. Identify what a Type I and Type II error would be in this scenario and give a consequence of each.
Type I: The average recovery time is 123.7, but the physician concludes that the average recovery time is greater than 123.7 days.
Consequence: The physician stops having patients use the cream, which causes more pain without actually speeding up the healing process.
Type II: The average recovery time is greater than 123.7 days, but the physician concludes that the average recovery time is equal to 123.7 days.
Consequence: The physician allows patients to continue using the cream, which causes patients to have a longer healing process.