Circles - What Key Feature do you see here?
Vertex
Triangles - Draw a graph to match this equation.
y = x2
Parabola - "U" shaped graph at vertex (0,0)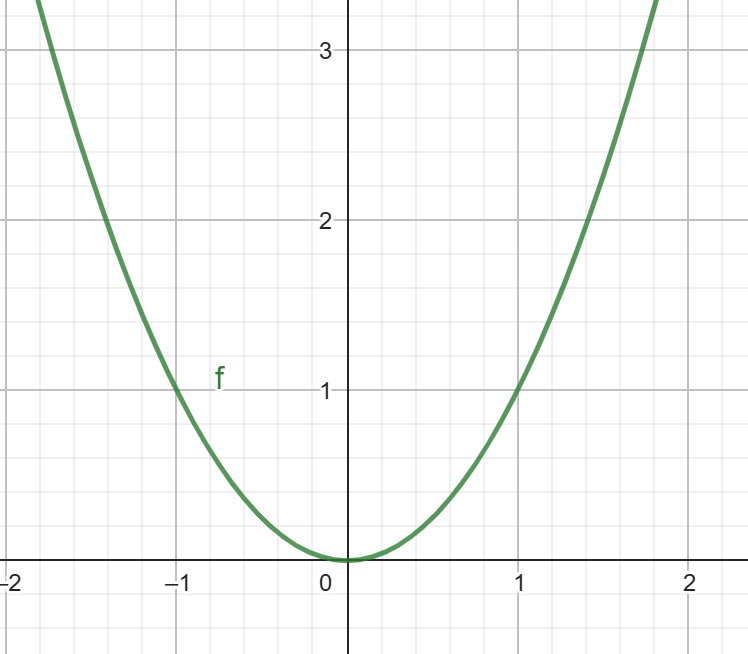
Write the equation for the following graph.
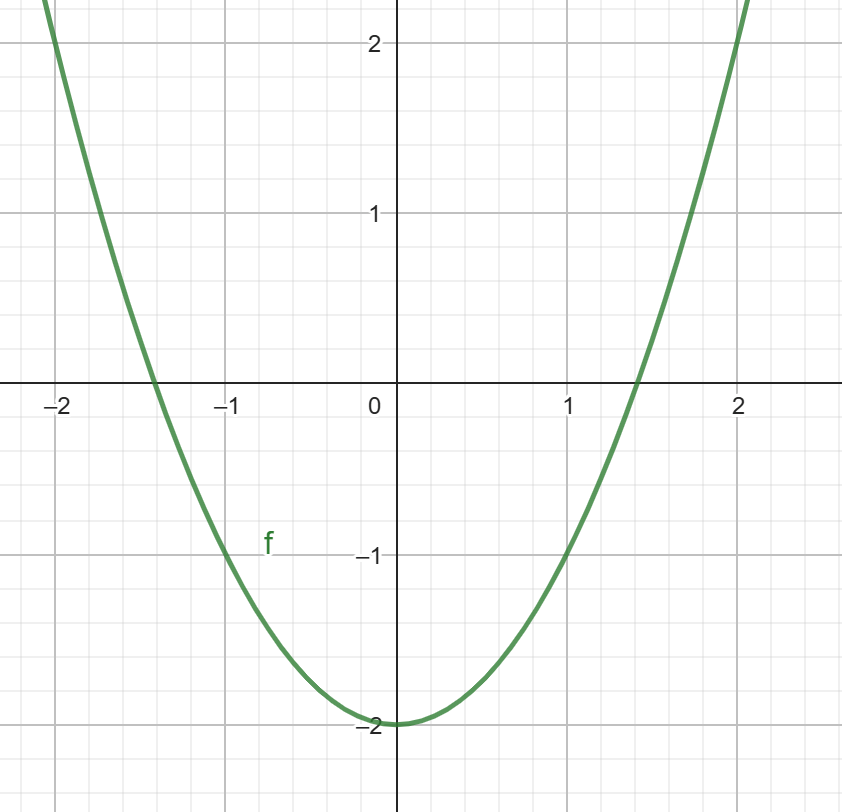
y = x2 - 2
Describe what would happen on the graph y = x2
if you change the equation to y = -x2.
The graph would be reflected over the x-axis.
Which of the following shows the formula for a function f(x)=x2 that is shifted three units to the right? SHOW ALL YOUR STEPS.
a. y = x2 - 6x + 9
b. y = x2 + 6x + 9
c. y = x2 - 6x - 9
a. y = x2 - 6x + 9
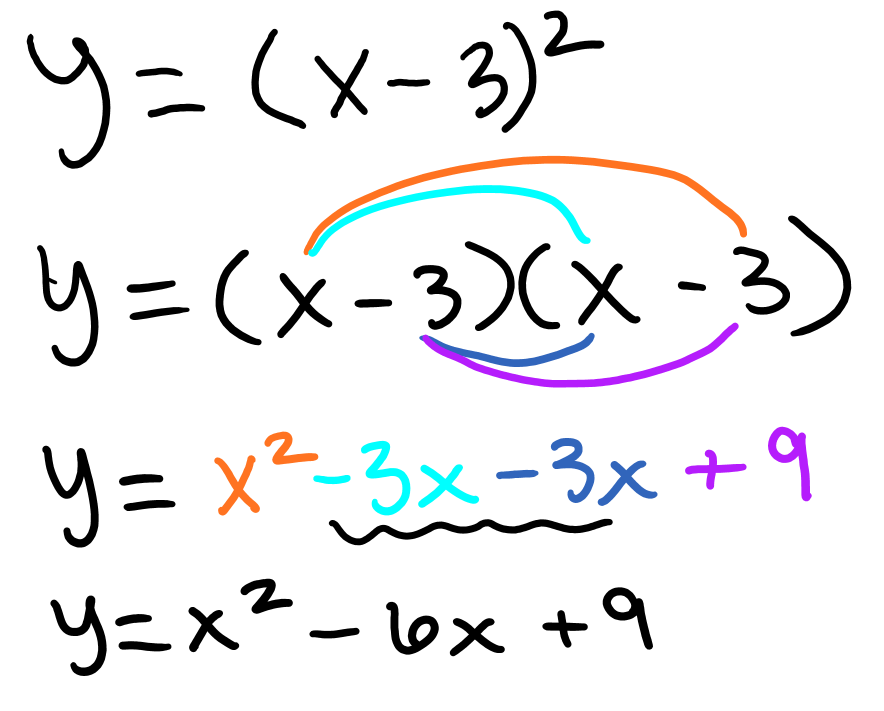
Another name for this key feature.
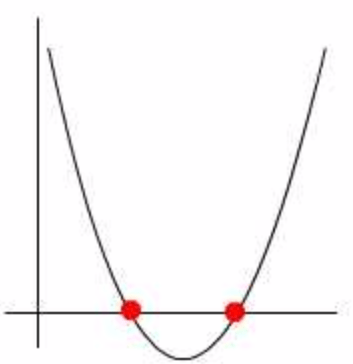
X-intercept, Zeros, or Roots
Triangles - This is where the graph passes the y-axis, like the point (0,3) seen here.

y-intercept
a. y = |x - 2|
b. y = (x - 2)2
c. y = (x - 2)3
I know that because...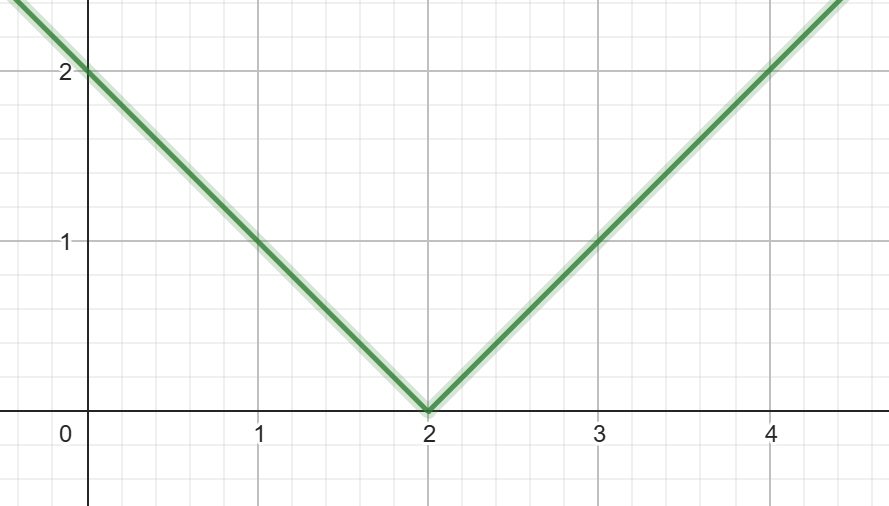
The absolute value bars make a V-shaped graph.
Describe what would happen on the graph y = x2
if you change the equation to y = (x - 2)2.
Draw it out for an extra 50 bonus points.
The graph would shift 2 units to the right along the x axis. Changing the "inside" of the equation shifts it left and right; oppoit of what you would expect.
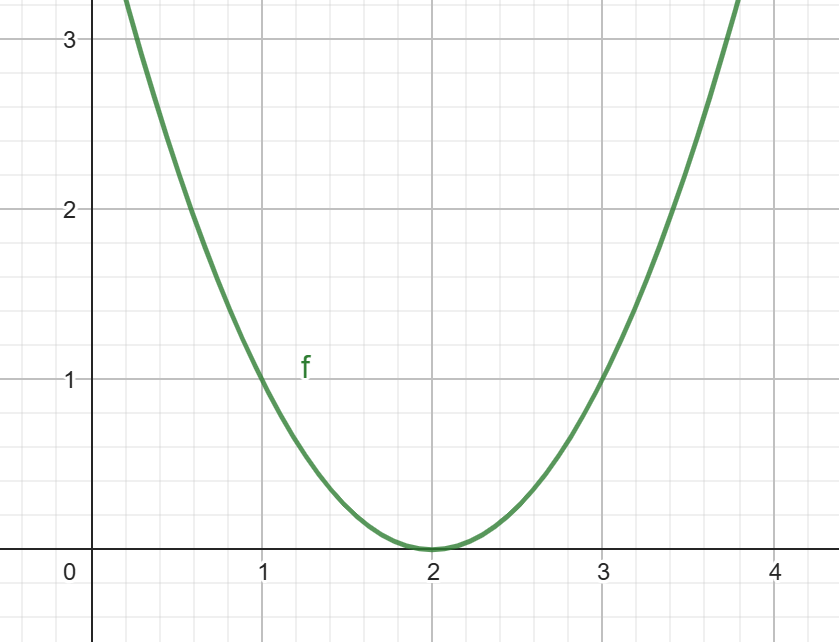
Write a formula for the functions that reflects
y = (x+2)2 - 2 over the y-axis.
y = (x - 2)2 - 2
Which of the following shows the formula for a function f(x)=x2 that is shifted one units to the left and three units down on a coordinate plane? SHOW ALL YOUR WORK.
a. x2 + 2x + 1
b. x2 - 2x - 2
c. x2 + 2x - 2
c. x2 + 2x - 2
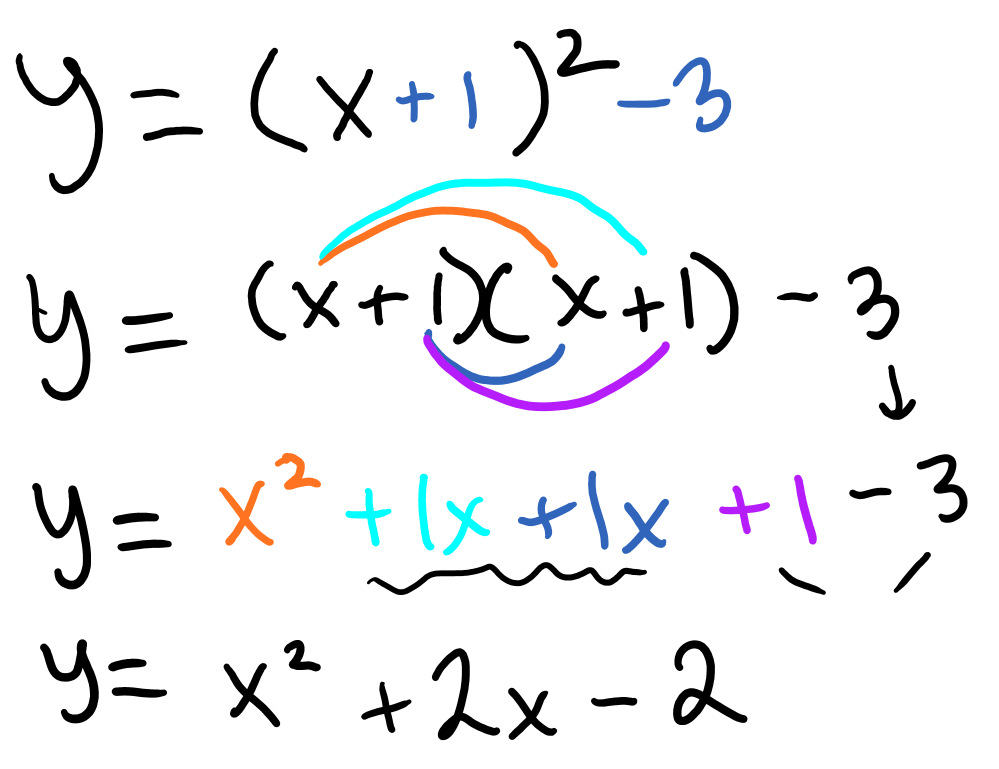
The quadratic function f(x)=x2 + 10x + 21 can be factored into the following form: f(x)=(x+3)(x+7) What are the x-intercepts of the function?
a. (-7, 0) and (-3, 0)
b. (0, -3) and (0, -7)
c. (3, 0) and (7, 0)
a. (-7, 0) and (-3, 0)
Triangles - This Key Feature is often noted as a dotted line down the middle of a graph to so that one side reflect the other.
Axis of Symmetry
a. y = |x| + 1
b. y = x2 + 1
c. y = x3 + 1
I know that because...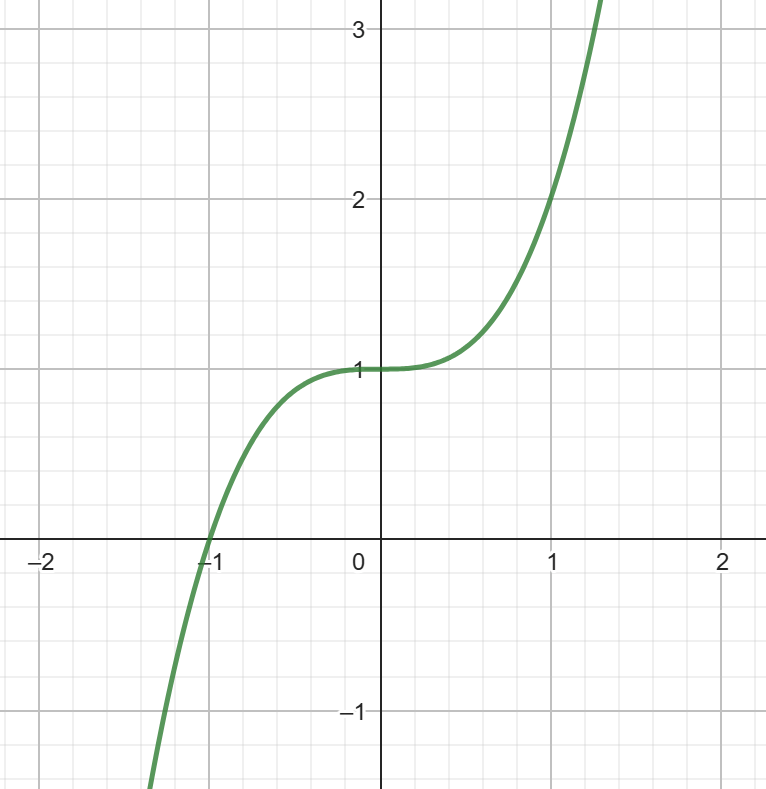
The odd exponent makes an "S" shape graph.
Describe what would happen on the graph y = x2
if you change the equation to y = (x + 4)2 - 2.
Draw it out for an extra 50 bonus points.
This graph would be shifted to the left 4 and down 2.
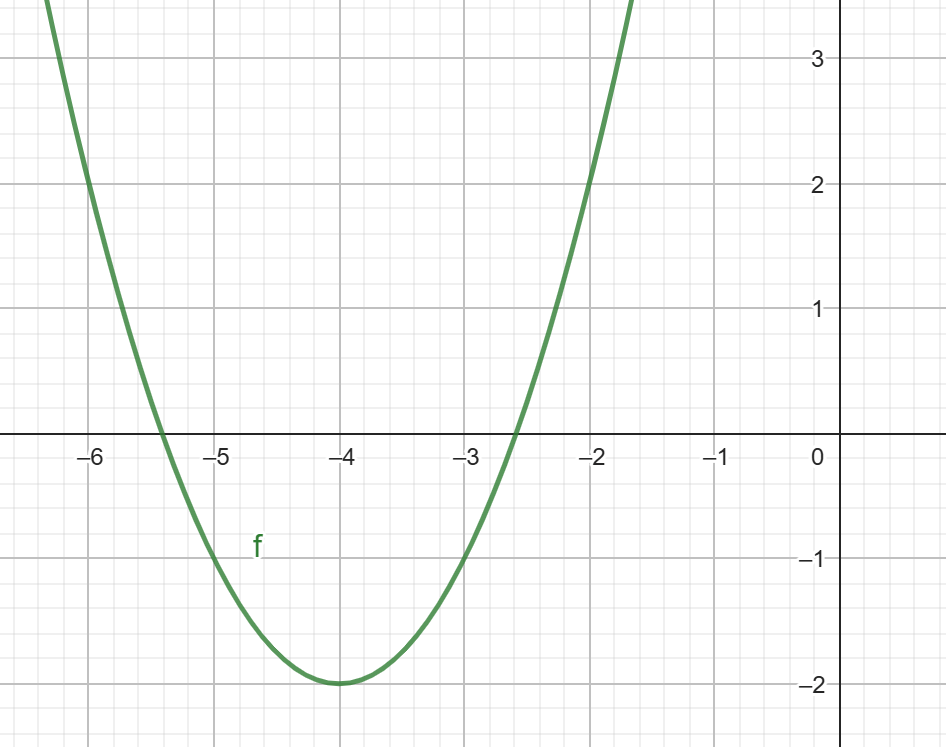
Write a formula for the functions that reflects
y = (x - 2)2 + 3 over the x-axis.
y = -(x - 2)2 - 3
Which of the following shows the formula for a function f(x)=x2 that is shifted four units to the right and two units up on a coordinate plane? SHOW ALL YOUR WORK.
a. x2 + 8x + 16
b. x2 - 8x + 18
c. x2 - 8x - 18
b. x2 - 8x + 18
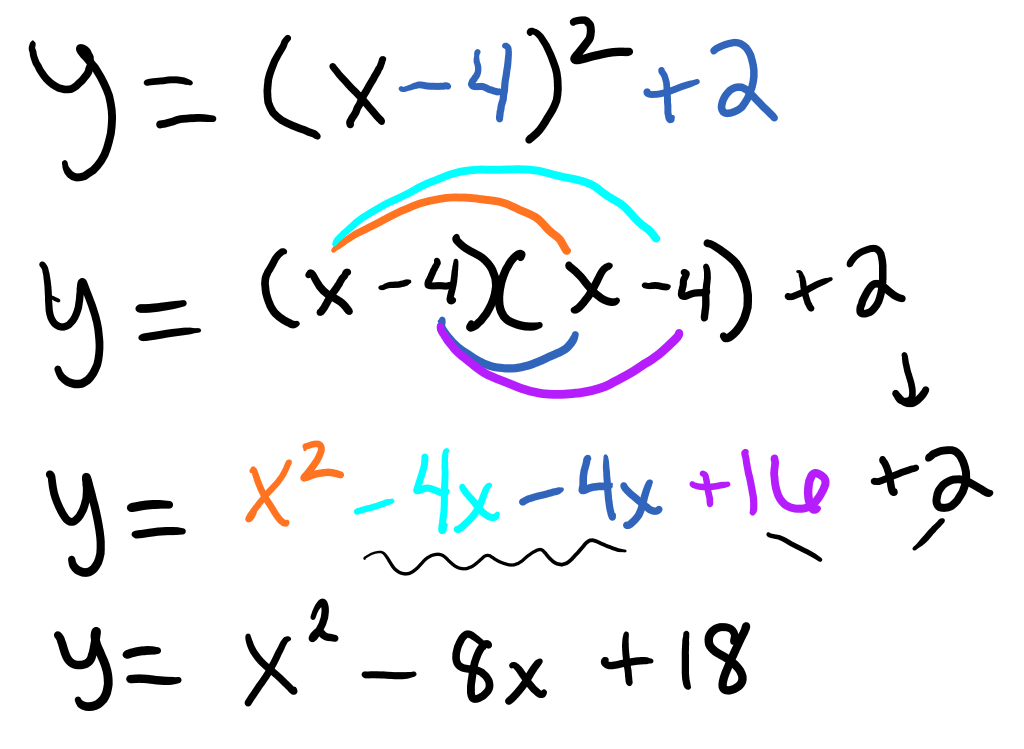
The quadratic function f(x)=x2 − 5x − 24 can be factored into the following form: f(x)=(x−8)(x+3) What are the x-intercepts of the function?
a. (-3, 0) and (0, 8)
b. (8, 0) and (-3, 0)
c. (-8, 0) and (3, 0)
b. (8, 0) and (-3, 0)
Circles - Label each key feature.
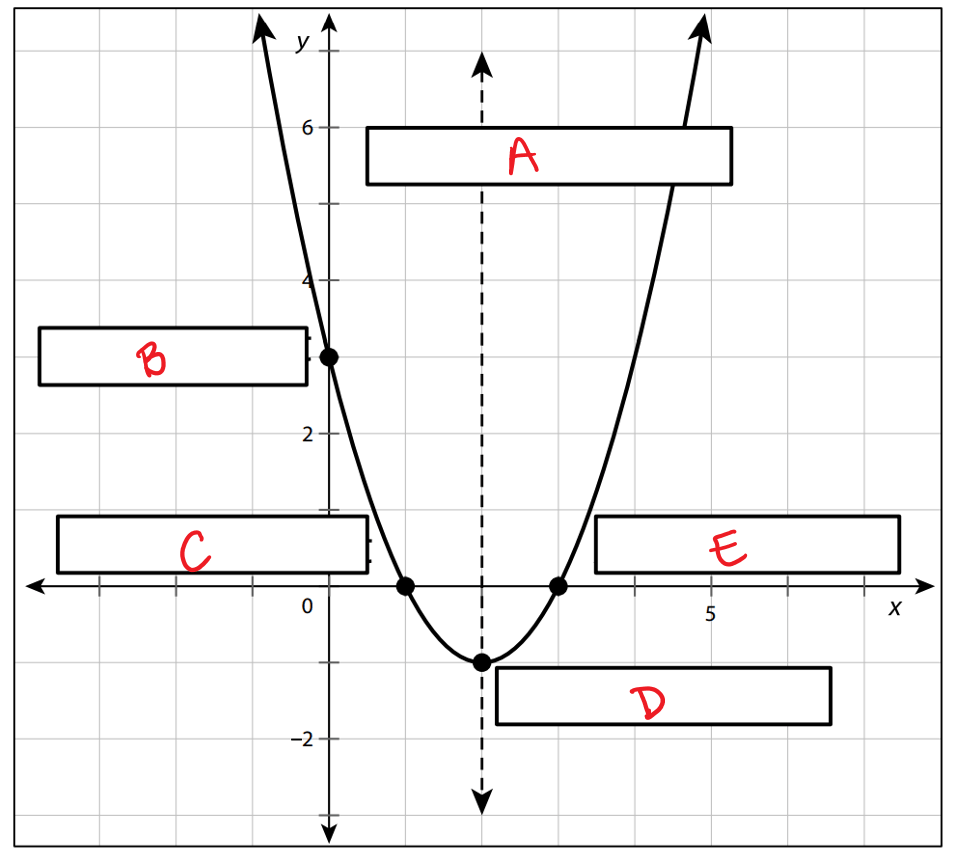
A. Axis of Symmetry
B. y - intercept
C. x - intercept (zero or root)
D. Vertex (on the axis of symmetry)
E. x - intercept (zero or root)
a. y = (x + 3)3
b. y = -(x - 3)3
c. y = (x - 3)3
I know that because...
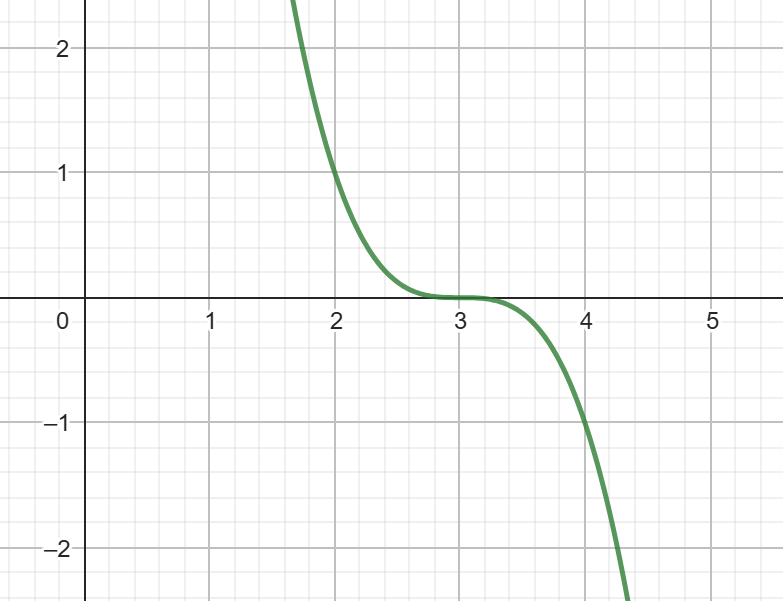
b. y = -(x - 3)3
Write an equation in Vertex form form that show the equation y = x2 shifted six units to the left and nine units down.
Bonus 200 points is you can convert to standard form.
y = (x + 6)2 - 9
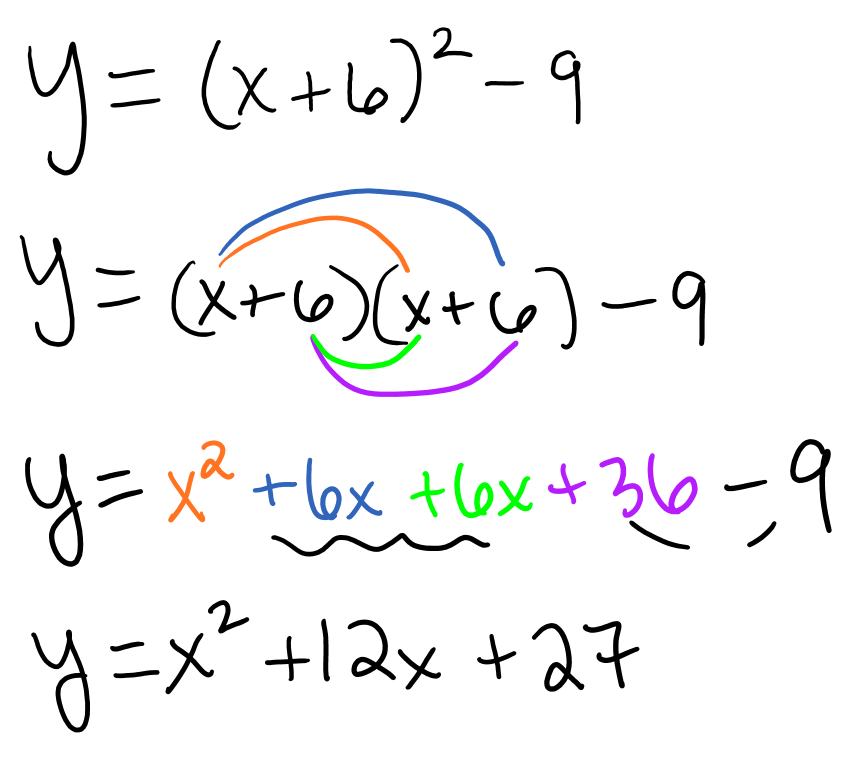
Which axis is the graph reflected over if the equation
was originally y = (x - 3)2 and the new equation
is y = -(x - 3)2. How do you know?
This is a reflection over the x-axis because the negative is on the "outside" of the equation.
Which of the following shows the formula for a function f(x)=x2 that is shifted seven units to the right and eight units down on a coordinate plane? SHOW ALL YOUR WORK.
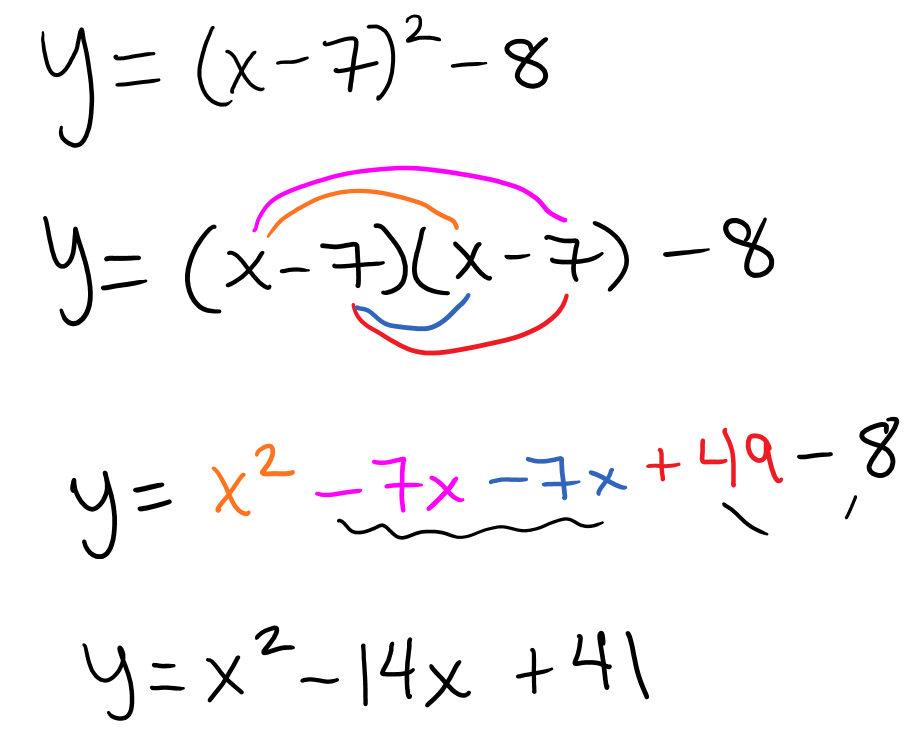
The quadratic function f(x)=x2 − 3x − 18 can be factored into
the following form: f(x)=(x−6)(x+3).
What are the x-intercepts of the function?
(6, 0) and (-3, 0)