Rules of Angles
Naming Pairs of Angles
Finding Variables in Angles
100
Can a pair/group of angles be both complementary AND supplementary?
Explain why or why not.
No, they cannot.
A pair/group of angles cannot both equal 90 degrees and 180 degrees at the same time.
100
Are these angles complementary or supplementary?
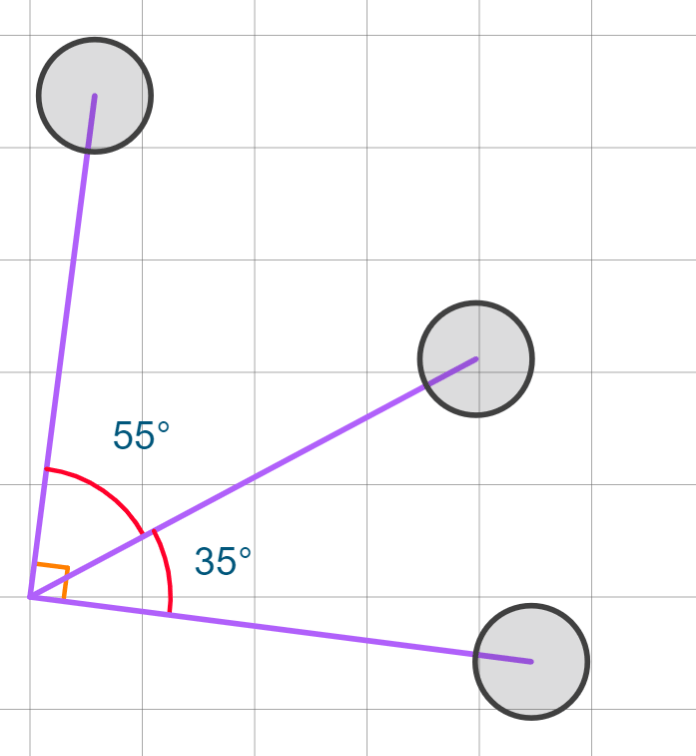
Complementary. They together form a perfect corner, or 90 degrees.
100
Find the value of angle a.
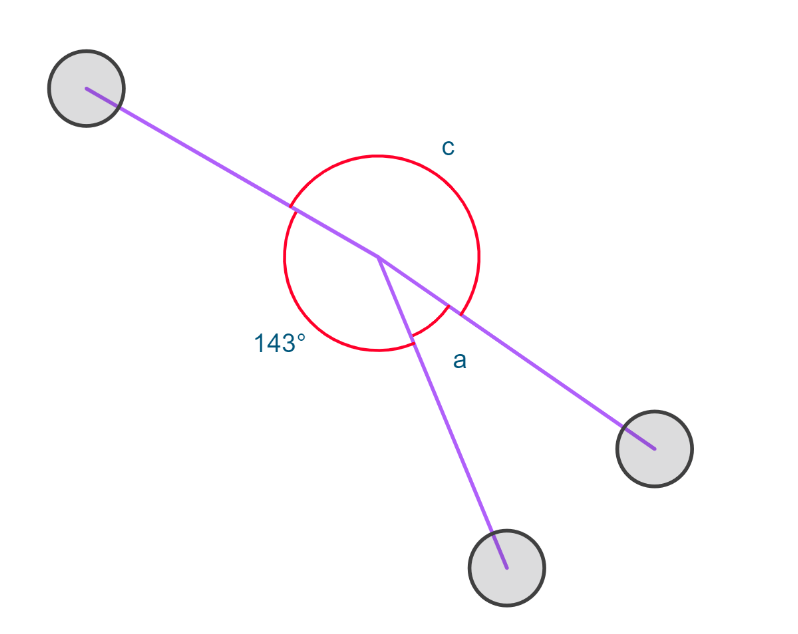
Angle a = 37 degrees.
200
Can a pair/group of angles be both vertical and supplementary?
Yes, but very rarely.
The only way vertical angles can also be supplementary is when added up they still equal 180 degrees.
200
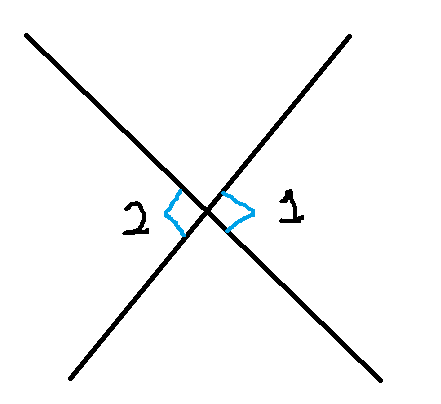
Are angles b and d vertical or adjacent with each other?
b and d are vertical with each other. They are straight across from each other.
200
If line segment jl runs perpendicular with line segment kl, how many degrees is angle klj?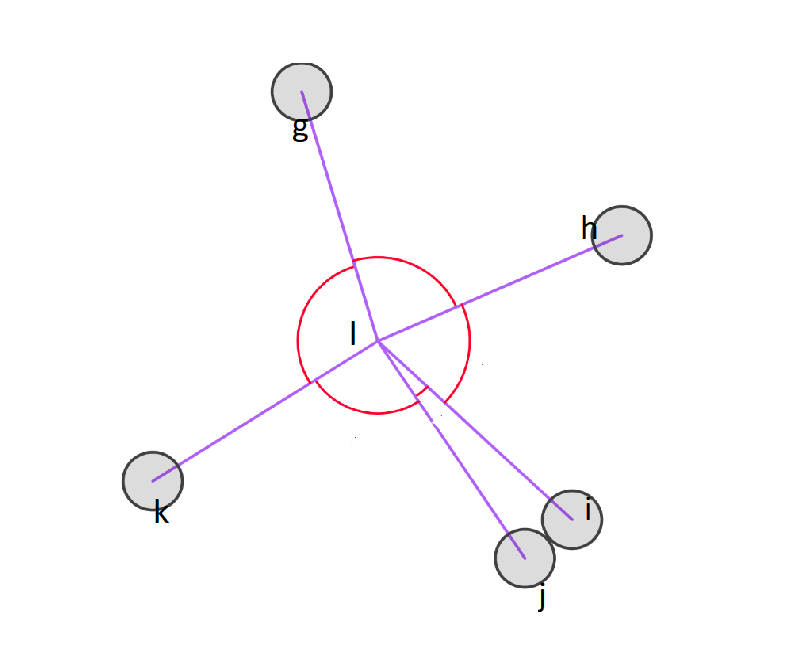
Angle klj is 90 degrees.
300
If angles are vertical they are always also...
Congruent. (the same size)
300
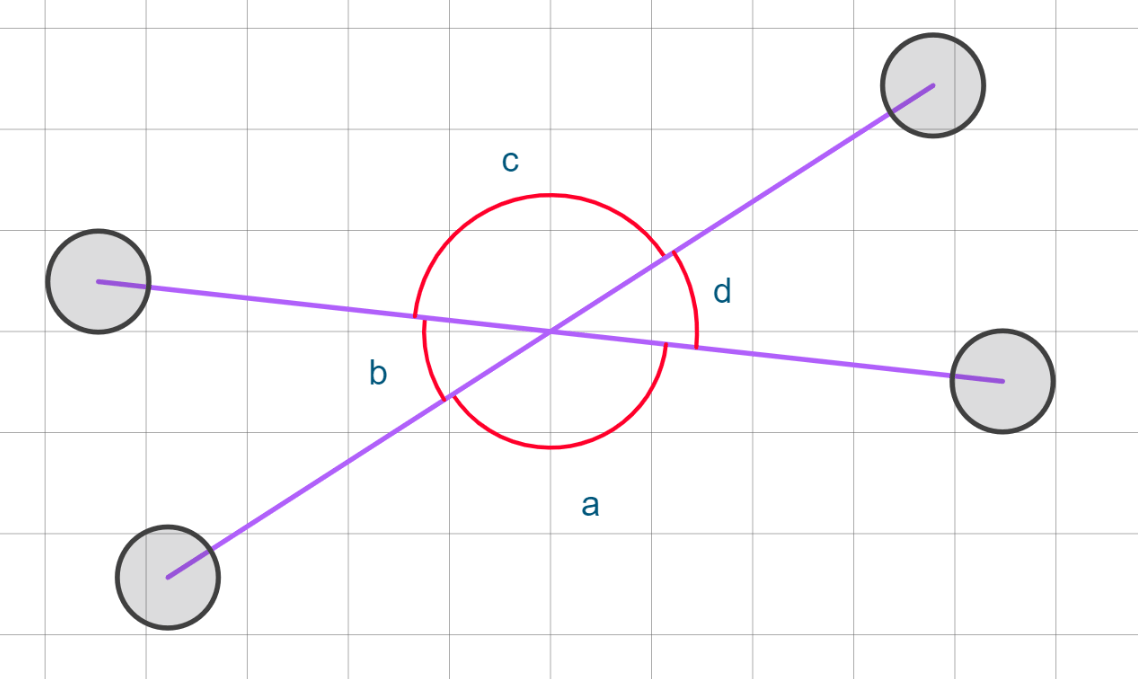
Would the sum of angles c and d be 90 degrees or 180 degrees?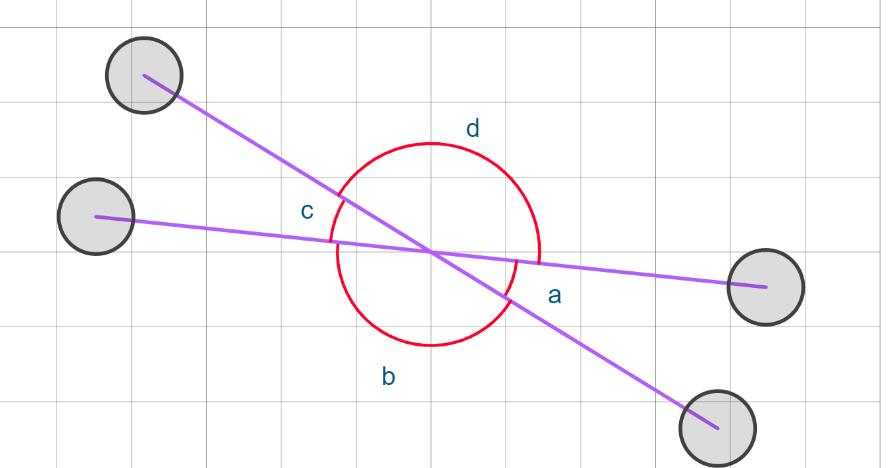
They would equal 180 degrees.
300
Find the value of just angle c.
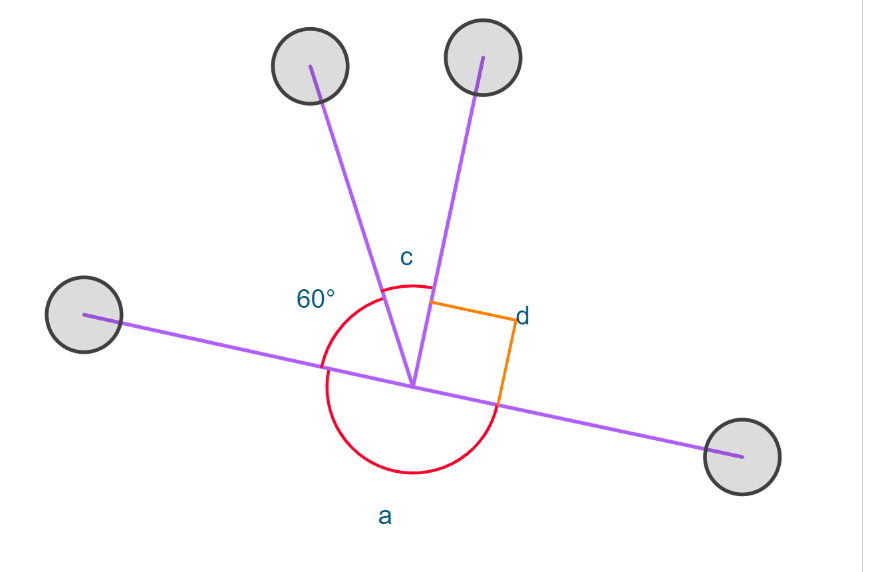
Angle c = 30 degrees.
400
Can a pair/group of angles be both vertical and adjacent?
Explain why or why not.
No, they cannot.
You cannot have angles be next to each other and across from each other at the same time.
400
Name all the possible kinds of angles c and d are with each other.
Angles c and d are supplementary, adjacent, and congruent.
400
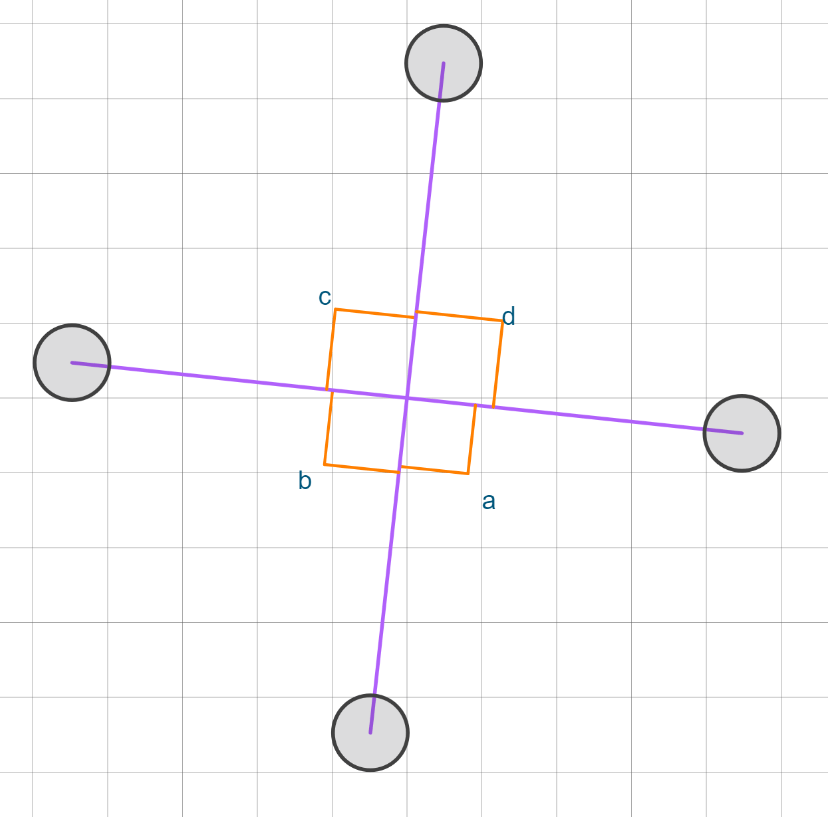
Find the values of both angles e and b.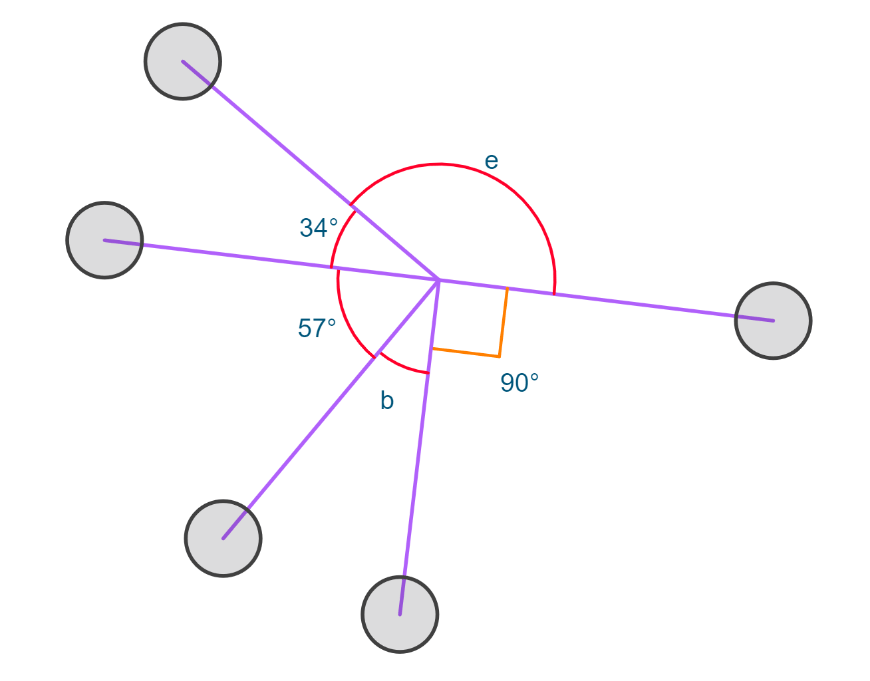
e = 146 degrees.
b = 33 degrees.
500
Can a group/pair of angles be congruent, complementary, and adjacent?
If yes, prove it be drawing an angle pair that is all of the above.
If no, please explain what cannot be true about this statement.
Yes this can happen.
500
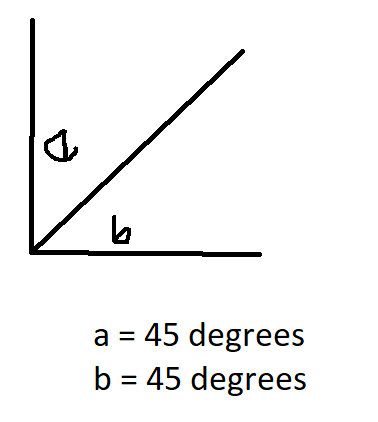
List all of the possible pairing names for angles e and a.
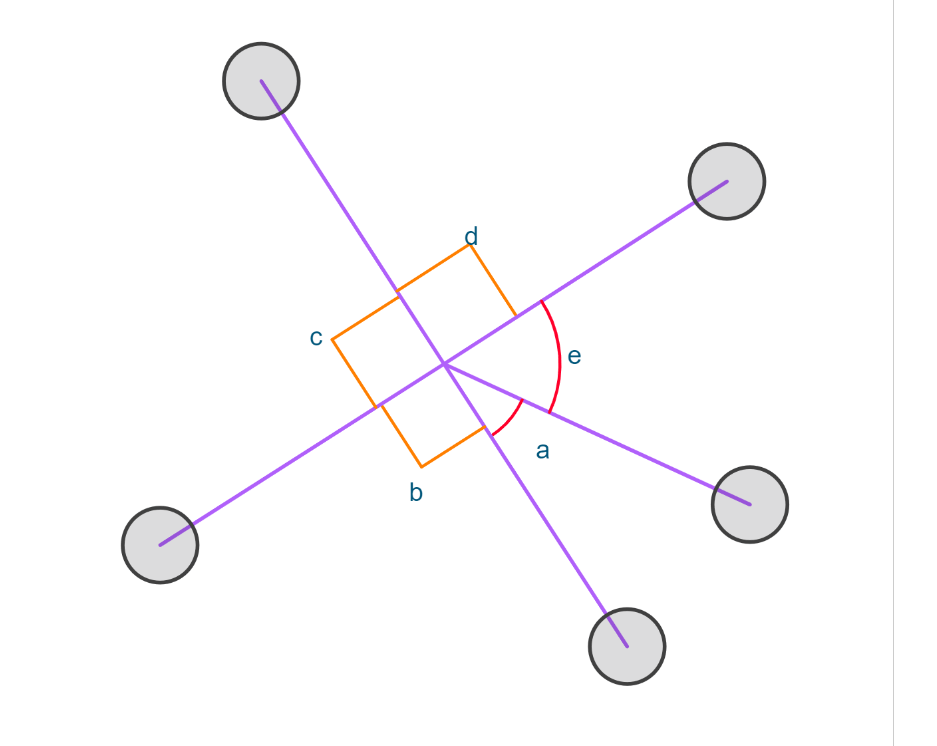
Adjacent and complementary.
500
Find the values of both angles b and c.
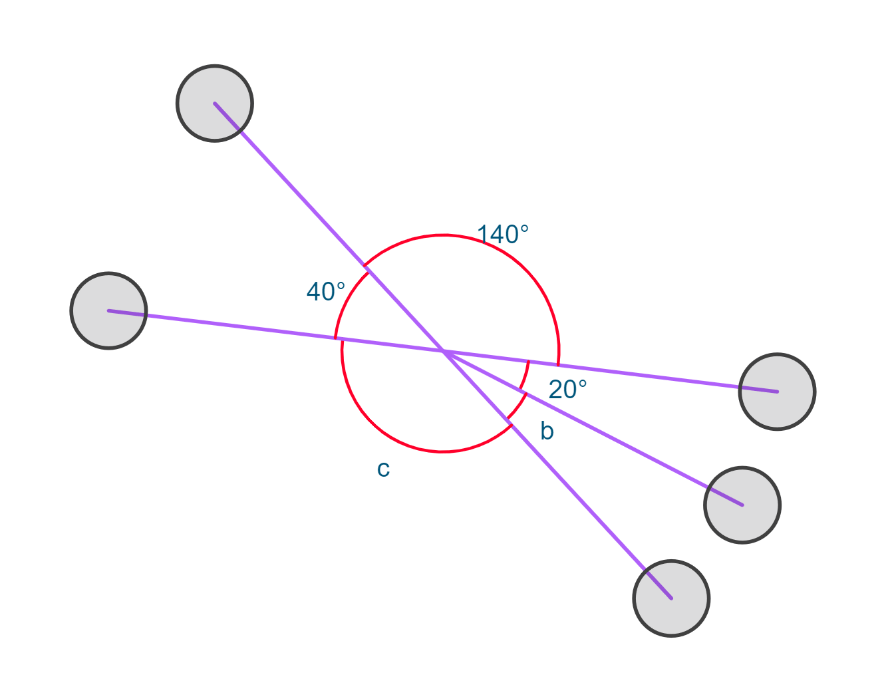
c = 140 degrees.
b = 20 degrees.