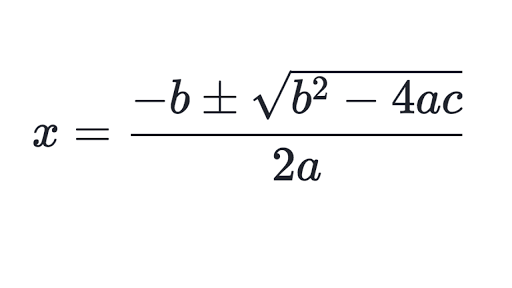What are the solutions to this quadratic function
(x-5)(x+3)=0
x = 5
x = -3
Explain why we need a plus or minus sign when solving quadratic equations such as x2 = 25
You can square the positive and negative number to make the equation true. There are 2 solutions
Rewrite this equation into standard form
3x2 - 5x = -10
3x2 - 5x + 10 = 0
Solve this quadratics by factoring to find the x-intercepts.
x2 + 2x - 3 = 0
x2 + 2x - 3 = 0
(x-1)(x+3) = 0
x = 1 or x = -3
Given the polynomial y = x2 − 6x + n. Find the value of n to make it a perfect trinomial
n = 9
Identify the a, b, and c value for this equation
m2 + 2m − 12 = 0
a = 1, b = 2, and c = -12
Solve this quadratics by factoring to find the x-intercepts.
X2 + 16 = 10x
x = 2 or x = 8
Solve this equation by taking square roots.
(x-4)2 - 16 = 0
(x-4)2 = 16
x- 4 =± 4
x = 0 or 8
Solve 2x2 = 7x + 6 by using quadratic formula.
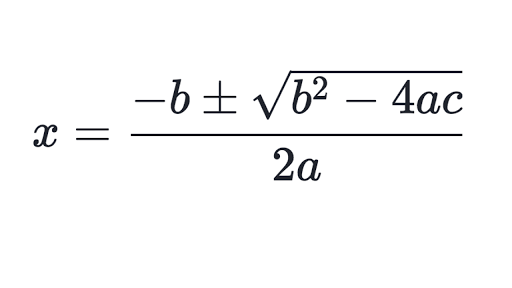
a = 2, b = -7, and c = -6
x = -(-7) ±√(-7)2 -4(2)(-6) / 2(2)
x = (7 ±√ 97) / 4
x =4.21 and -.71
Draw a parabola that only has one solutions
Look at board
Find the mistake of the following complete the square problem
1) x2−6x=3
2) x2−6x+(−3)2=3+9
3) (x−3)2=12
4) x−3=±12
5) x=15 and -12
In the step 4, they forgot to take the square root of 12
Solve x2 + 4x - 21 = 0 by using quadratic formula.
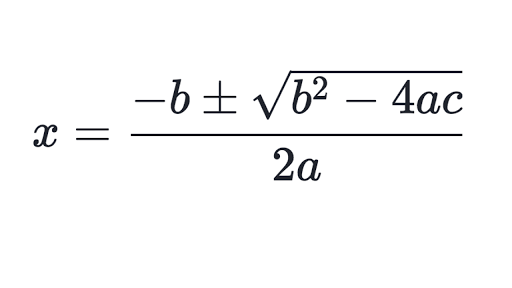
a = 1, b = 4, and c = -21
x = 3 or -7
If the solution to a quadratic function is x = -2 and x = 4, write the equation in factored form
y = (x + 2)(x - 4)
Solve x2 - 6x + 7 = 0
x2 - 6x = -7
x2 -6x + (3)2 = -7 + 9
x2 -6x + 9 = 2
(x-3)2 = 2
x -3 = ± √2
x = 4.42 and 1.59
Solve x2 - 8x + 14 = 0 using the quadratic formula.
a = 1, b = -8, and c = 14
x = -(-8) ±√ (-8)2 - 4(1)(14) / 2(1)
= 8 ±√ 8 / 2
= 5.41 and 2.59