Circles & Polygons
Volume
Surface Area
Composite Shapes
100
Find the area of sector GCH below. Round to two decimal places and include units.
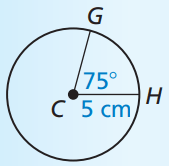
A = \theta/360\times\pir^2
A = 75/360\times\pi(5)^2
A = 16.36 cm^2
100
Find the volume of the oblique triangular prism below.
V=Bh
V=(1/2\times7\times10)(5)
V=175 ` cubic inches`
100
Find the surface area of the square-based pyramid below.
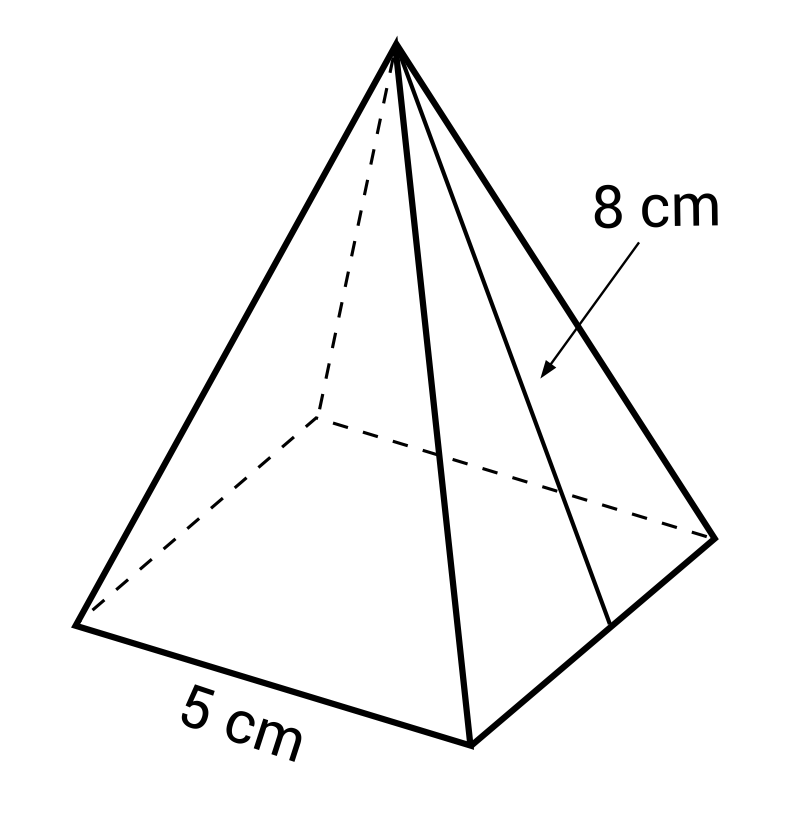
SA=(5)^2 + 4(1/2\times5\times8)
SA=25+4(20)
SA=105 cm^2
100
Find the volume of the solid below. Round to two decimal places.
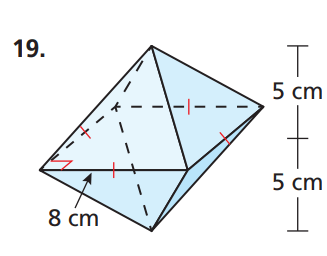
V=2(1/3Bh)
V=2(1/3(8^2)(5))
V=213.33 cm^3
200
Find the area of the regular dodecagon (12 sides) below. The length of each side is 9 inches.
200
Find the height of the cylinder below.
V=pir^2h
4608pi=pi(12)^2h
4608=144h
h=32 ` inches`
200
Find the surface area of this hemisphere. Leave your answer in terms of pi.
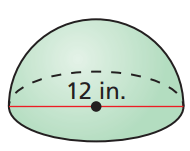
SA=1/2(4pir^2)+pir^2
SA=2pi(6)^2+pi(6)^2
SA=72pi+36pi=108pi` sq. in.`
200
Find the volume of the composite shape below.
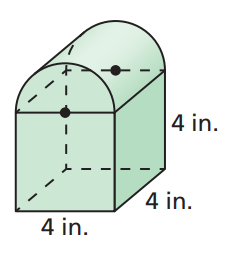
V_(Cyl)=1/2(pir^2h)
V_(Cyl)=1/2(pi(2)^24)
V_(Cyl)=25.13
V_(Cu)=Bh=(4^2)(4)=64
V=64+25.13
V=89.13` cubic inches`
300
Find the radius of the circle below given the central angle and arc length of the major (larger) arc LM.
AL = \theta/360\times2pir
38.95=260/360\times2pir
38.95=4.538r
r=8.58 cm
300
Find the volume of the sphere below.
C=2pir
7pi=2pir
7=2r
r=3.5
V=4/3pir^3
V=4/3pi(3.5)^3
V=179.59` cubic inches`
300
The cone below has a volume of 216π in3. Find the surface area.
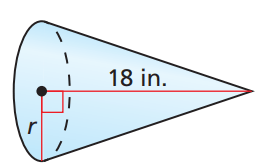
V=1/3pir^2h
216pi=1/3pir^2(18)
216=6r^2
36=r^2 ` so ` r=6
6^2+18^2=l^2
l=18.97
SA=pir^2+pirl
SA=pi(6)^2+pi(6)(18.97)
SA=470.74` sq. in.`
300
*DAILY DOUBLE*
Find the surface area of the composite solid below. Round to two decimal places.
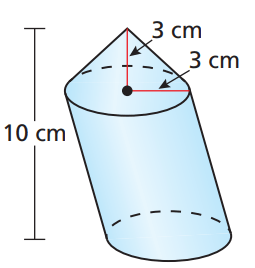
SA_[Co]=pirl
SA_[Co]=pi(3)(3\sqrt(2))
SA_[Co]=39.99 cm^2
SA_[Cyl]=pir^2+2pirh
SA_[Cyl]=pi(3)^2+2pi(3)(7)
SA_[Cyl]=160.22 cm^2
SA = 200.21 cm^2
400
Find the area of a regular icosagon (20 sides) with a perimeter of 160 feet.
`Each side`= 160/20=8` ft`
`Each triangle`=360/20=18^o
tan(9) = 4/a
a = 4/tan(9) = 25.255
A_T = 1/2(8)(25.255) = 101.02
A_I = 101.02\times 20 = 2020.4 ft^2
400
Find the volume of the square-based pyramid below.
h^2+2.5^2=8^2
h=7.6
V=1/3Bh
V=1/3(5^2)(7.6)
V=63.33 cm^3
400
Find the surface area of the green solid shown below. Round to two decimal places.
SA=2(`sector`)+2(`flat side`)+` curved side`
A_S=78/360\timespi(4)^2
A_S=10.89
A_[FS]=4\times 10=40
`Arc`=78/360\times2pi(4)
`Arc`=5.445
A_[CS]=5.445\times 10 = 54.45
SA=2(10.89)+2(40)+54.45
SA= 156.24 m^2
400
Find the volume of the shape below.
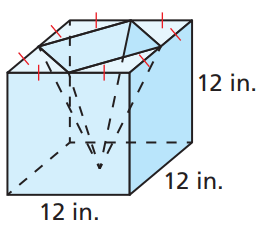
V_C=Bh=(12^2)12=1728
`Pyramid base side length`
s=6\sqrt(2) ` (isosceles)`
V_P=1/3Bh
V_P=1/3(6\sqrt(2))^2(12)
V_P=288
V=1728-288=1440` cubic inches`
500
***FINAL JEOPARDY***
Find the surface area of the hexagonal pyramid below.
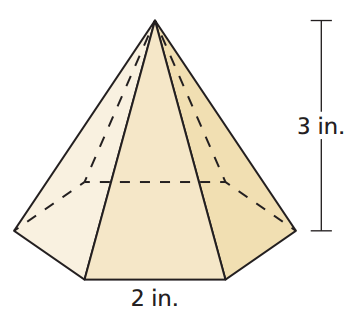
L^2=sqrt(3)^2+3^2
L=3.46
A_H=1/2(2)(\sqrt(3))\times 6
A_H=10.39
A_T=(1/2)(2)(3.46)\times 6
A_T=20.78
SA=10.39+20.78=31.18` sq. in.`