True/False
Fill in the Blank
Problems
III.3
III.12
100
A line drawn between two points on the circumference of the circle must fall within the circle.
True
(III.2)
100
A _________ is a line segment whose endpoints are 2 points on the circumference of the circle.
Chord
100
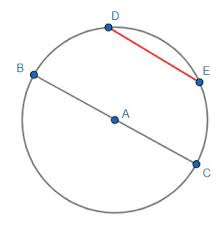
In circle ABC, diameter AB bisects chord CD at E. The center of the circle is O. if OE = 10 in and AB = 40 in,.
What is the name of the theorem that gives us the information we need to solve this problem?
Diameter Chord Theorem
100
If a straight line passing through the center of a circle bisects a straight line not passing through the center, then it also cuts it at right angles.
What theorem is this proposition proving?
Diameter Chord Theorem
100
If two circles touch one another externally, then the straight line joining their centers passes through the point of contact.
What kind of proof is this?
An indirect proof.
200
In a circle, the greater chord is further from the center.
False
(The biggest is the diameter in the middle, as you get further the chords get shorter)
200
A _______________ is a line which, when extended, meets the circle at only one point.
Tangent
200
In circle ABC, diameter AB bisects chord CD at E. The center of the circle is O. if OE = 10 in and AB = 40 in.
Since the diameter bisects the chord, what else must the diameter do to the chord?
Cut it at right angles
200
If a straight line passing through the center of a circle bisects a straight line not passing through the center, then it also cuts it at right angles.
What are we given?
CD a diameter, AB a chord but not a diameter, CD bisects AB.
200
If two circles touch one another externally, then the straight line joining their centers passes through the point of contact.
What is given?
Circles ABC and ADE touching externally at point A.
300
Two circles tangent internally share a common center.
False
(III.11)
300
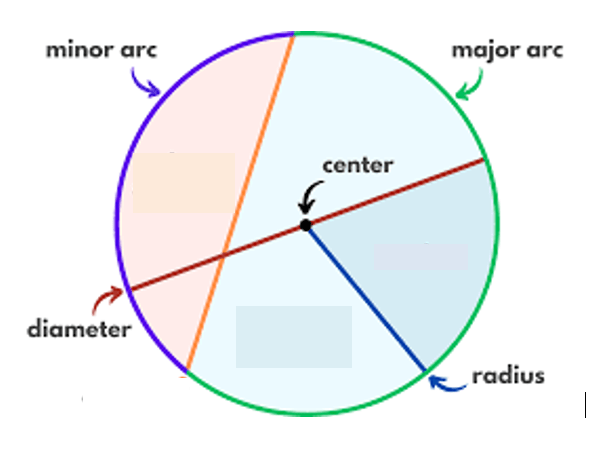
The largest version of a chord passes through the ______________ of the circle and is called the ___________________.
1. Center 2. Diameter
300
In circle ABC, diameter AB bisects chord CD at E. The center of the circle is O. if OE = 10 in and AB = 40 in.
Since the diameter AB is also perpendicular to Chord CD, what kind of triangles must OCE and ODE be? What theorem can we use to solve this problem due to this?
1. Right Triangles 2. Pythagorean Theorem
300
If a straight line passing through the center of a circle bisects a straight line not passing through the center, then it also cuts it at right angles.
What are we trying to prove?
CD is perpendicular to AB
300
If two circles touch one another externally, then the straight line joining their centers passes through the point of contact.
What are we trying to prove?
The line that joins the centers of the circles passes through point A.
400
A diameter which intersects a chord must bisect the chord at right angles.
False
(The diameter must also intersect perpendicularly)
400
A _____________ arc is greater than a semicircle, while a __________ arc is less than a semicircle.
1. Major 2. Minor
400
In circle ABC, diameter AB bisects chord CD at E. The center of the circle is O. if OE = 10 in and AB = 40 in. Find the length of CE.
CE =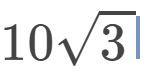
400
If a straight line passing through the center of a circle bisects a straight line not passing through the center, then it also cuts it at right angles.
What should the very last step of this proof be?
CD is perpendicular to AB
400
If two circles touch one another externally, then the straight line joining their centers passes through the point of contact.
How many steps are in the construction?
3
500
The distance between the centers of two tangent circles is equal to either the sum or the difference of the lengths of the two radii.
True
500
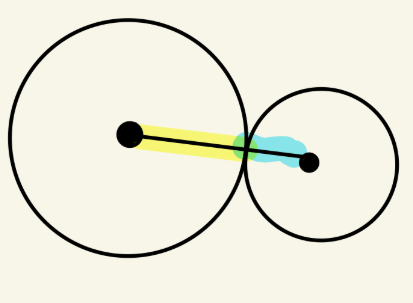
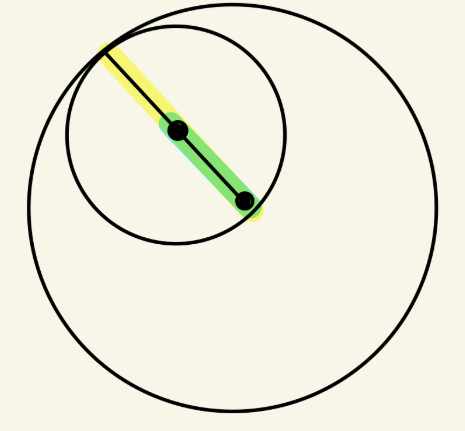
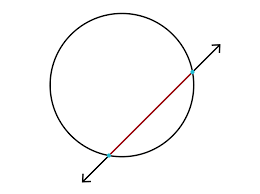
A _______________ is a line which, when extended, meets the circle at two points.
Secant
500
In circle ABC, diameter AB bisects chord CD at E. The center of the circle is O. if OE = 10 in and AB = 40 in, find the length of chord CD.
CD =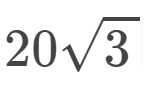 
500
If a straight line passing through the center of a circle bisects a straight line not passing through the center, then it also cuts it at right angles.
What congruence theorem must be used to prove this?
SSS [Side-Side-Side]
500
If two circles touch one another externally, then the straight line joining their centers passes through the point of contact.
What should be the last step in the proof?
FG passes through A.