Exponential Growth/Decay
The Number e
Intro to Logs
Properties of Logs
Exponential and Log Equations
100
Is the following growth, decay, or neither?
y=5(1/3)^x
Decay
100
Simplify. Your answer should contain only positive exponents.
-2e^(3x)*e^(-4)
-2e^(3x-4)
100
Rewrite in exponential form.
log14(196) = 2
142 = 196
100
Use a calculator to approximate to the nearest thousandth. Use the change of base formula to show work.
log3(42)
log(42)/log(3) = 3.402
100
Solve by getting the same bases:
(1/25)^(2m-6)=125^(m+1)
m=9/7
200
Is the following growth, decay, or neither?
y=-3(1/4)^-x
Growth
200
Simplify. Your answer should contain only positive exponents.
(5e^x)/(e^(5x))
5/e^(4x)
200
Rewrite in log form.
32 = 9
log3(9) = 2
200
Expand the following log:
log(x^6y^5)
6logx+5logy
200
Solve:
-5+logn=-6
n=1/10
300
Write down three coordinate points for the following graph. Begin with the "base function" using x=0,1,2
y=3(2)^(x-1)+2
(1,5)
(2,8)
(3,14)
300
Is the following exponential growth or decay?
y=-1/7(1/e)^(-x)
Growth
300
Evaluate without a calculator:
log3(27)
3
300
Expand the following log:
ln(x/(y^5z))^6
6lnx-30lny-6lnz
300
Solve and round to 3 decimal places:
-ln(-x)=-2
x=-7.389
400
Give the percent increase or decrease for the following equation:
y=1.5(0.45)^x
Decrease of 55%
400
Write the model and then answer the question.
You deposit $1,000 in an account that pays 2% annual interest compounded quarterly. How much will you have after 10 years?
A=1,000(1+.02/4)^(4t) =$1,220.79
400
Evaluate without a calculator:
log5(1/25)
-2
400
DAILY DOUBLE!!!!
Condense to a single log:
loga+logb+logc/3+logd/3
400
Solve and write the exact answer and rounded to 3 decimal places:
3^(x-5)=12
x = log3(12)+5
x = 7.262
500
Write the model and answer the following question. Round to the nearest hair.
Mr. Wilson has 135 gray hairs on his head. If the amount of gray hair is increasing by 13% every year from teaching high school algebra, how many gray hairs will he have after 20 years of teaching algebra?
y=135(1.13)^x 1,556 gray hairs
500
Write the model and then answer the question.
You deposit $1,000 in an account that pays 2% annual interest compounded continuously. How much will you have after 10 years?
A=1,000e^(.02t)=$1,221.40
500
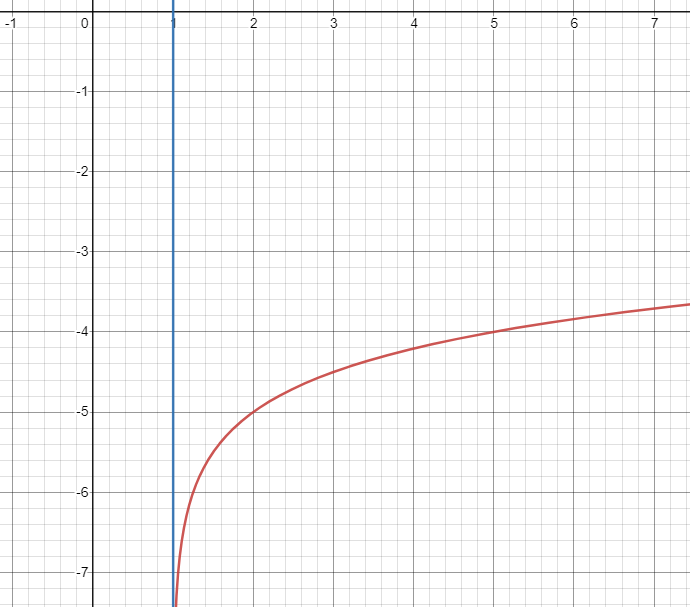
List 3 points of the following graph, sketch the graph, and identify the domain and range. Write the equation and label the asymptote. Without a calculator!
f(x)=log4(x-1)-5
(2,-5), (5,-4), (17,-3) D: x>1 R: All Real Numbers
Asymptote: x=1
500
Condense to a single log:
5lnw-5lnu-15lnv
ln(w^5/(u^5v^15))
500
Solve and write the exact answer and rounded to 3 decimal places:
-7e^(-9x-8)-9=-39
x=-(ln(30/7)+8)/9=-1.051