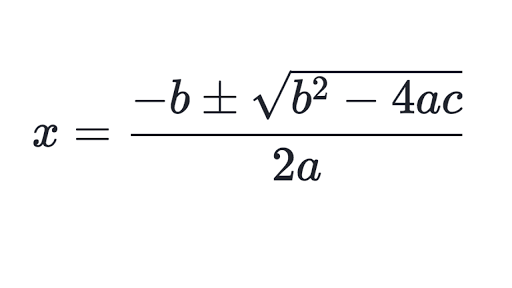What's the first step to solve quadratics by factoring
Step 1. Write the equation in standard form.
What's the first thing you have to do to complete the square?
Make sure that it is written in standard form and = to 0
ax2 + bx + c =0
(Remember, when y is 0 you will find the x-intercepts) (x,0)
When solving using the quadratic formula, what is the first 2 things you should do?
1st - make sure it is in standard form
(ax2 + bx + c = 0
2nd - Write down the values of;
a =
b =
c =
What do you have to do first to solve quadratics equation by taking square roots?
Isolate the square.
How is standard form written for a quadratic equation?
y = ax2 + bx + c
or
ax2 + bx + c = 0
Where is the vertex located?
At the point where the axis of symmetry cross the the parabola.
What do you have to do after you write the equation in the standard form?
Step 2. Factor completely.
Step 3. Use the zero product property.
Step 4. Solve each factor to get the x.
Rewrite in vertex form y = x2 − 6x by completing the square.
x2 − 6x = 0
x2 − 6x + 9 = 0 + 9
(x -3)2 = 9
y = (x-3)2 -9
Solve using the quadratic formula for this equation;
2m2 + 2m − 12 = 0
a = 2, b = 2, and c = -12
x = -(2) ±√ (2)2 - 4(2)(-12) / 2(2)
x = 2 and -3
Solve this equation by taking square roots.
x2 + 1 = 37
x2 = 36
x= 6, -6
How is vertex form written for a Quadratic Equation?
y = a(x-h)2 + k
or
a(x-h)2 + k = 0
What is the formula to find Axis of Symmetry?
x=-b/2a
Solve this quadratics by factoring to find the x-intercepts. (Hint: box method from unit 7 notes)
x2 + 2x = 3
x2 + 2x - 3 = 0
(x-1)(x+3) = 0
x = 1 or x = -3
Rewrite in vertex form y = x2 − 25 by completing the square.
x2 − 25 = 0
x2 = 25
(x)2 = 25
y = (x)2 - 25
Solve x2 + 4x - 21 = 0 by using quadratic formula.
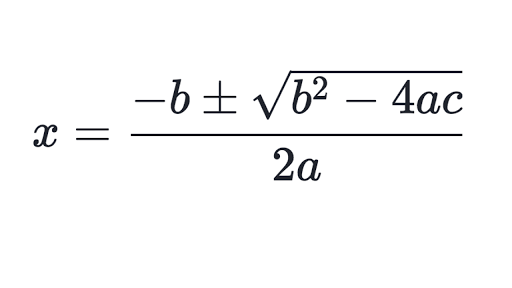
a = 1, b = 4, and c = -21
x = 3 or -7
Solve this equation by taking square roots.
x2 - 10 = 54
x2 = 64
x = 8 , -8
What is the formula for x-vertex coordinate when the quadratic equation is in standard form?
x =- b/(2a)
What is equation of the parent function of a quadratic equation?
y=x2
Solve this quadratics by factoring to find the x-intercepts. (Hint: box method from unit 7 notes)
X2 + 16 = 10x
x2 - 10x + 16 =0
(x-2)(x-8)
x = 2 or x = 8
Rewrite in vertex form x2 − 6x − 3 = 0 by completing the square.
x2−6x=3
x2−6x+(−3)2=3+9
(x−3)2 = 12
y =(x−3)2 - 12
Solve x2 - 8x + 14 = 0 using the quadratic formula.
a = 1, b = -8, and c = 14
x = -(-8) ±√ (-8)2 - 4(1)(14) / 2(1)
= 8 ±√ 8 / 2
= 5.41 and 2.59
Solve this equation by taking square roots.
(x-4)2 - 16 = 0
(x-4)2 = 16
x- 4 =± 4
x = 0 or 8
What is the formula for the vertex when the quadratic equation is in vertex form?
(-h, k)
TWO!
Solve this quadratics by factoring to find the x-intercepts. (Hint: box method from unit 7 notes)
18x2 - 3x = 6
18x2 - 3x -6 = 0
= 3(6x2 - x - 2) = 0
= 3(3x -2)(2x +1)= 0
= 3x -2 = 0 2x + 1 = 0
x = 2/3 or x -1/2
Rewrite in Vertex form x2 - 6x + 7 = 0 by using completing the square
x2 - 6x = -7
x2 -6x + (3)2 = -7 + 9
x2 -6x + 9 = 2
(x-3)2 = 2
y = (x-3)2 - 2
Solve 2x2 = 7x + 6 by using quadratic formula.
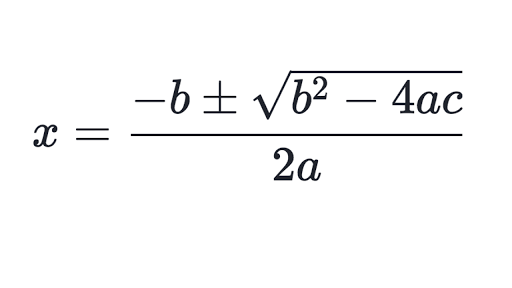
a = 2, b = -7, and c = -6
x = -(-7) ±√(-7)2 -4(2)(-6) / 2(2)
x = (7 ±√ 97) / 4
x =4.21 and -.71
Solve this equation by taking square roots.
(x+7)2 - 11 = 0
(x+7)2 = 11
x + 7 = ±√11
x = -3.68 and -10.32
("a value"uarr or darr)/(1harr)
When the discriminate is less than zero, how many times does the parabola cross the x-axis?
None.