Graphing
Slope-Intercept Form
Solve with Elimination
Solve with Substitution
Word Problems
100
Graph the following:
y= 2x - 1
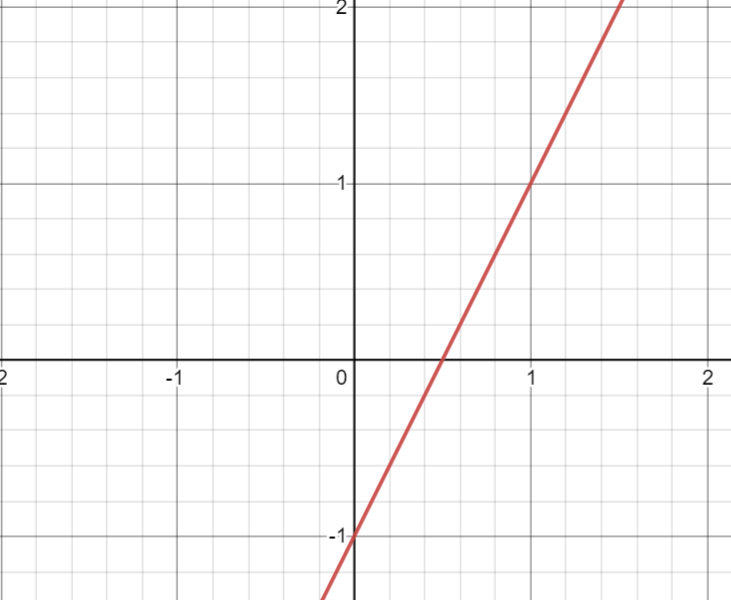
Your graph should look like this!
100
y= 6x -4
What is the slope?
What is the y-intercept?
Slope: 6
Y-Intercept: -4
100
Solve with Elimination:
−3y+5x=26
−2y−5x=−16
(4, -2)
100
Solve with substitution:
y= -2x + 14
y=5x -7
(3, 8)
100
A canoe rental service charges a $20 transportation fee and $30 dollars an hour to rent a canoe. Write and graph an equation representing the cost, y, of renting a canoe for x hours.
Y =30x + 20
Y= Total Cost
X = # of hours
200
Graph the following:
y = 1/4x + 3
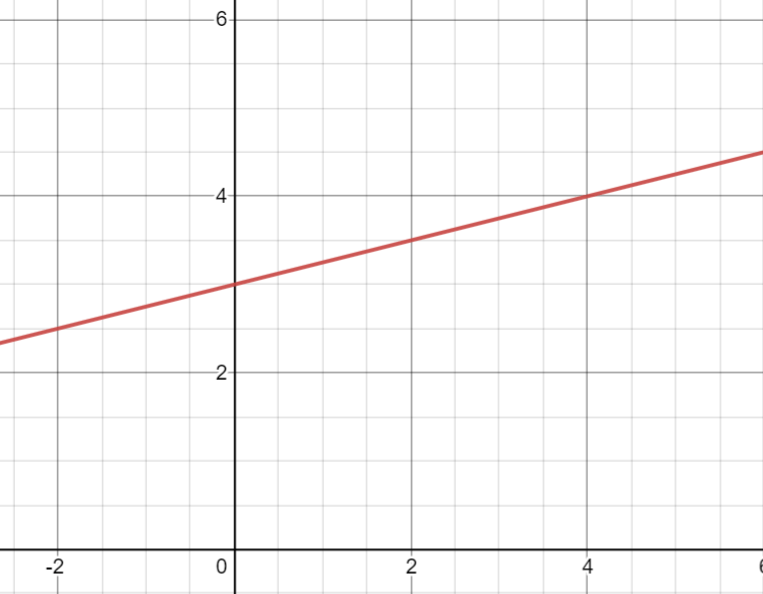
Your graph should look like this!
200
Rewrite in slope-intercept form:
-2x + y = 1
y= 2x + 1
200
Solve with elimination:
−8y+9x=−5
8y+7x=−75
(-5, -5)
200
Solve with substitution:
x-y = -9
8x -3y = -62
(-7, 2)
200
Kayla tutors and works in the college bookstore to pay for her college tuition. She makes $20 per hour tutoring and $8.50 per hour working in the bookstore.
Write an equation to represent the total amount of money Kayla earns tutoring and working in the bookstore.
M=20t + 8.5b
M= Total money
T= Tutoring
B= Bookstore
300
Write the equation for the following line:
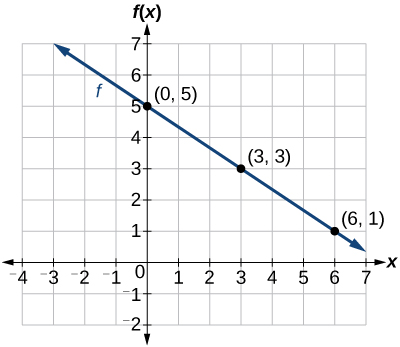
y = -2/3 x + 5
300
Rewrite in slope-intercept form:
4x – 2y = 12
y= 2x - 6
300
Solve with elimination:
8x + y = −16
−3x + y = −5
(−1, −8)
300
Solve with substitution:
2x= 16 - 8y
x + 4y =25
No Solution
300
Suppose that a bike rents for $4 plus $1.50 per hour. Write an equation in slope-intercept form that models this situation.
Then fill out the table below.
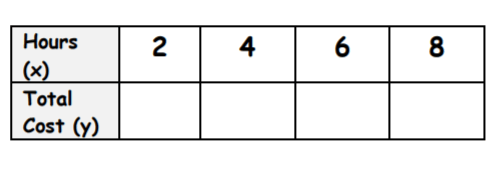
C = 1.50h + 4
C= total cost
H= # of hours
400
Graph the following equation:
2y = 6x - 8
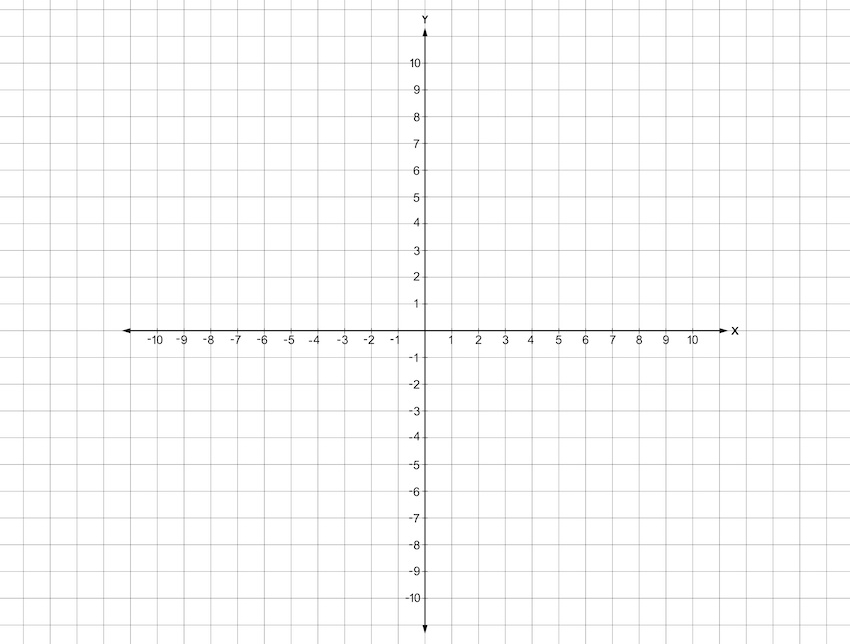
Your graph should look like this!
400
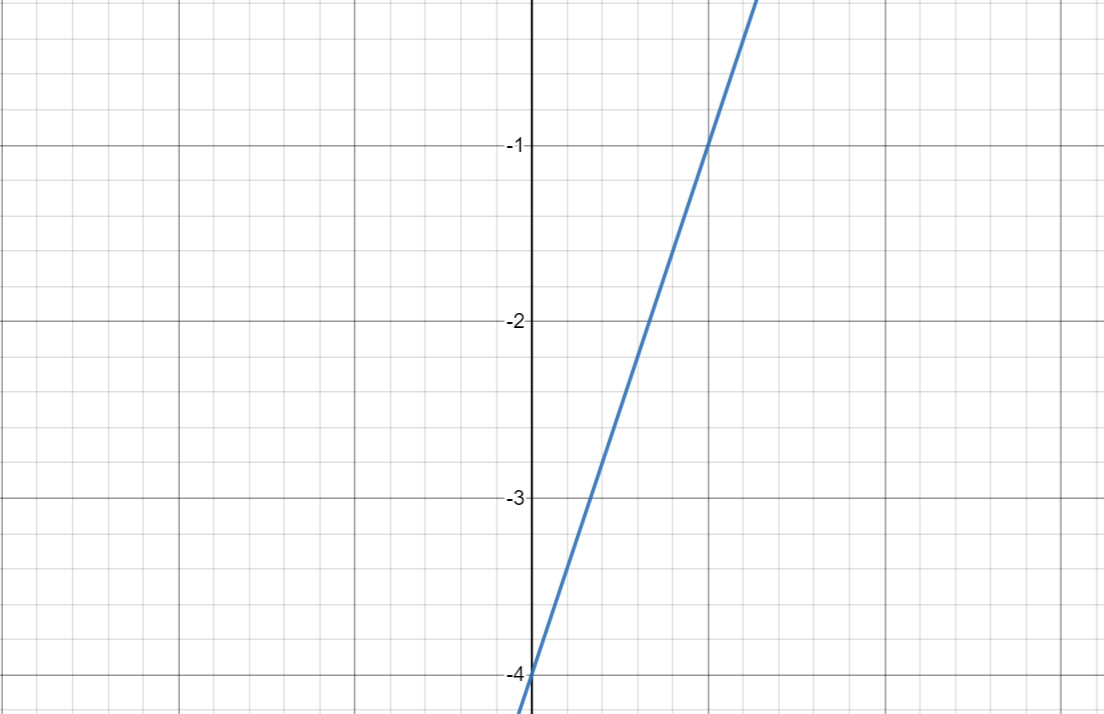
Rewrite in slope-intercept form:
x - 4y =28
y= 1/4 x -7
400
Solve using elimination:
5x + 12y = -34
2x + 4y = -12
(-2, -2)
400
Solve with substitution:
2x - 9y = 26
6x - 2y = -22
(-5, -4)
400
A video rental store charges a $20 membership fee and $2.50 for each video rented. Write and a linear equation to model this situation.
If 15 videos are rented, what is the revenue?
Y = 2.50x + 20
Y = Total revenue
X= # of videos rented
15 videos rented + membership: $57.50
500
Graph the following equation:
-y= 2/3x + 2
500
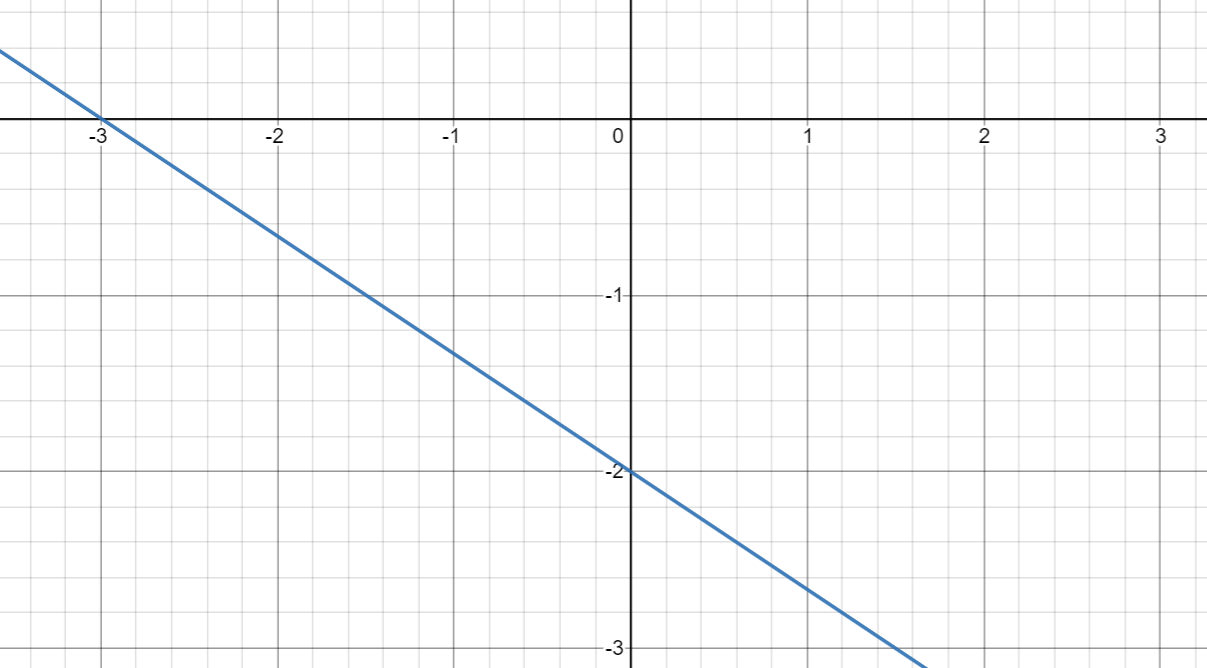
Rewrite in slope-intercept form:
9y -36 = -15x
y = -5/3 x + 4
500
Solve with elimination:
14x + 7y = -7
y= -2x - 1
Infinite Solutions
500
Solve with substitution:
3x - 2y = 10
9x + 4y = -50
(-2, -8)
500
Attorney A charges a fixed fee on $250 for an initial meeting and $150 per hour for all hours worked after that. Attorney B charges $150 for the initial meeting and $175 per hour. Write linear equations for both situations.
Find the charge for 26 hours of work for each attorney.
Which is the better deal?
Attorney A: c = 150h + 250
Attorney B: c= 175h + 150
After 26 hours, lawyer A costs $4,150 and lawyer B costs $4,700