What does f'(x)>0 tell us about the original function?
The function is increasing.
What does f''(x)<0 tell us about the original funtion?
The function is concave down.
Identify the absolute maximum
16
lim_(x->9) (x-9)/(x^2-81)
1/18
What is the domain of the price-demand function?
p=350-x/40
0<=x<=14,000
Identify the local extrema of the function.
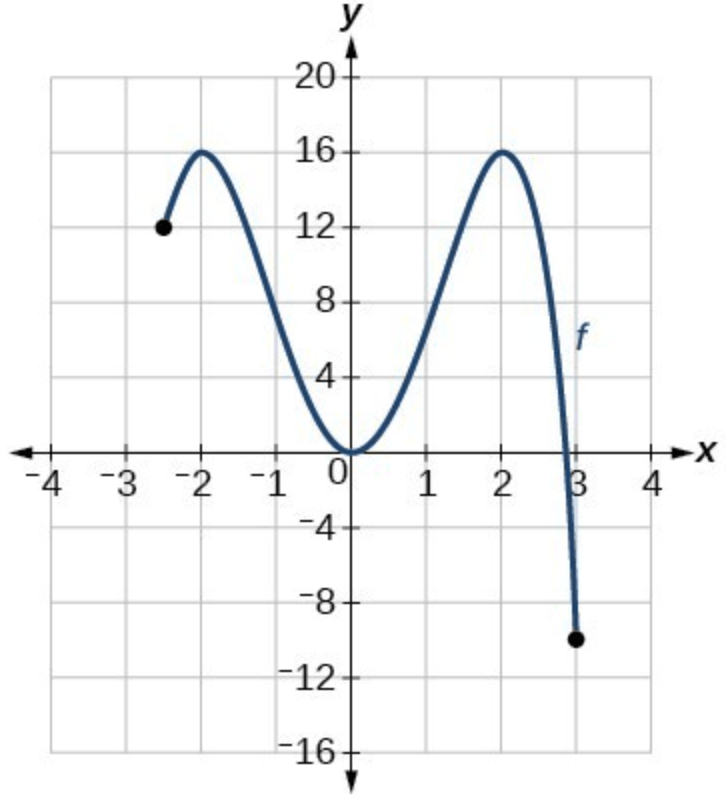
local max: 16
local min: 0
Sketch a graph that meets the following conditions.
f'(x)<0
f''(x)>0
the endpoints and critical numbers
lim_(x->4) (x^2+x-20)/(x-4)
9
A car rental agency rents 200 cars per day at a rate of $20 per day. For each $1 increase in rate, 5 fewer cars are rented.
Write the revenue function for the number of cars rented.
R(x)=(200-5x)(20+x)
R(x)=-5x^2+100x+4000
Find the intervals of increase and decrease.
f(x)=4+8x-x^2
increasing
(-oo,4)
decreasing
(4, oo)
Identify the intervals on which the function
f(x)=x^3-21x^2+17x+7
is concave up and concave down.
Concave down
(-oo, 7)
Concave up
(7, oo)
Find the absolute maximum and minimum values of the function over the indicated interval, and indicate the x-values at which they occur.
g(x)=x^2+4 [1,5]
absolute max of 29 at x=5
absolute min of 5 at x=1
lim_(x->oo) (x^11)/(lnx)
oo
A company manufactures and sells x cellphones per week. The weekly price-demand and cost equations are given below.
p=600-0.5x C(x)=20,000+140x
Write the profit function for the number of cell phones produced and sold.
P(x)=-0.5x^2+460x-20,000
Find the local extrema of
g(x)=x^3-75x-3
Local max of 247 at x=-5
Local min of -253 at x=5
Identify the intervals on which the function
f(x)=x^4-2x^3
is concave up and concave down.
Concave down
(0,1)
Concave up
(-oo,0), (1,oo)
Find the absolute minimum of
f(x)=9x^3-4
no absolute minimum
lim_(x->0) (e^(5x)-1)/(x^2+x)
5
A deli sells 960 sandwiches per day at a price of $8 each.
A market survey shows that for every $ 0.10 reduction in the price, 20 more sandwiches will be sold. How much should the deli charge in order to maximize revenue?
$6.40
Find the intervals of increase and decrease.
f(x)=5/(x^3+8)
decreasing
(-oo,oo)
Determine the point(s) of inflection. Write as ordered pairs. No rounding ;)
f(x)=-x^6+42x^5-42x+13
(0, 13)
(28, 240943989)
Find the absolute maximum and minimum values of the function over the indicated interval, and indicate the x-values at which they occur.
f(x)=x^4-8x^2+16 [-1,3]
absolute max of 25 at x=3
absolute min of 0 at x=2
lim_(x->4) (sqrt(x)-2)/(x^2-16)
1/32
A company manufactures and sells x cellphones per week. The weekly price-demand and cost equations are given below.
p=600-0.5x C(x)=20,000+140x
What price should the company charge for the phones maximize the weekly revenue?
$300