Understand the Features
Empirical Rule
Z-Score
100
What is the definition of mean?
The average of the data
100
What is the Empirical Rule and when can you use it?
68, 95, 99.7
When the data has normal distribution
100
What is the formula for z-score?
z= (expected value-mean)/standard deviation
200
What is the definition of mode and median
mode: piece of data that shows up the most
median: the middle of the data
200
If a population has a normal distribution, what percentage is one standard deviation of the mean?
68%
200
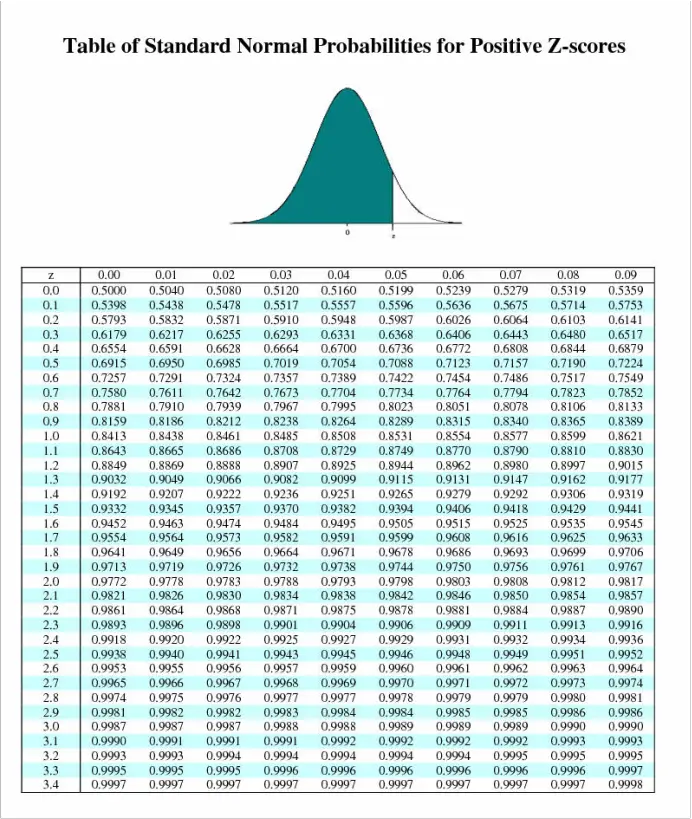
If the z score is 1.34, what is the probability on the z score table?
0.9099
300
Identify ALL the properties of a normal distribution.
Bell curve
Symmetrical (single peaked)
Mean in the middle
Not skewed to the left or right
Empirical Rule
300
The average height of middle school students is 58 inches with a standard deviation of 2 inches.
Find the probability of middle school students who are 58 inches and shorter
50%
300
Sally took two tests. On Test #1, she scored a 19 out of 25, and the mean score was 20 with a standard deviation of 3. On Test #2, she scored an 11 out of 15, and the mean score was 10 with a standard deviation of 2. Which test did she do better on?
Test #2 because it has a higher z score
test 1: (19-20)/3= -0.33333
test 2: (11-10)/2=0.5
400
Does this represent normal distribution? Why?
No because it does not resemble a bell curve, and it is double peaked.
400
The average dog lives 10 years with a standard deviation of 2 years.
FInd the probability of a dog who lives 6 years or less
2.5%
400
Sally has a vespa that has an average speed of 65 mph with a standard deviation of 4. What is the probability that the speed is less than 60 mph?
z= (60-65)/4
=-1.25
z score table: 0.1056
Probability= 0.1056
500
Sketch a normal distribution graph and label its properties.
500
The average lifespan of a giant panda is 15 years with a standard deviation of 3 years.
Find the probability of a panda who lives between 9-24 years
97.35%
500
Sally asked her classmates what they got on their math test. If the mean of her data was 81.1% with a standard deviation of 4.7, what is the probability of a student scoring more than 83%?
z = (83−81.1)/4.7
= 0.404
z score table: 0.6700
Probability: (1-0.6700)= 0.33