Vectors
Turn, turn, turn
Rivers, boats, planes, and air
Projectile Motion
200
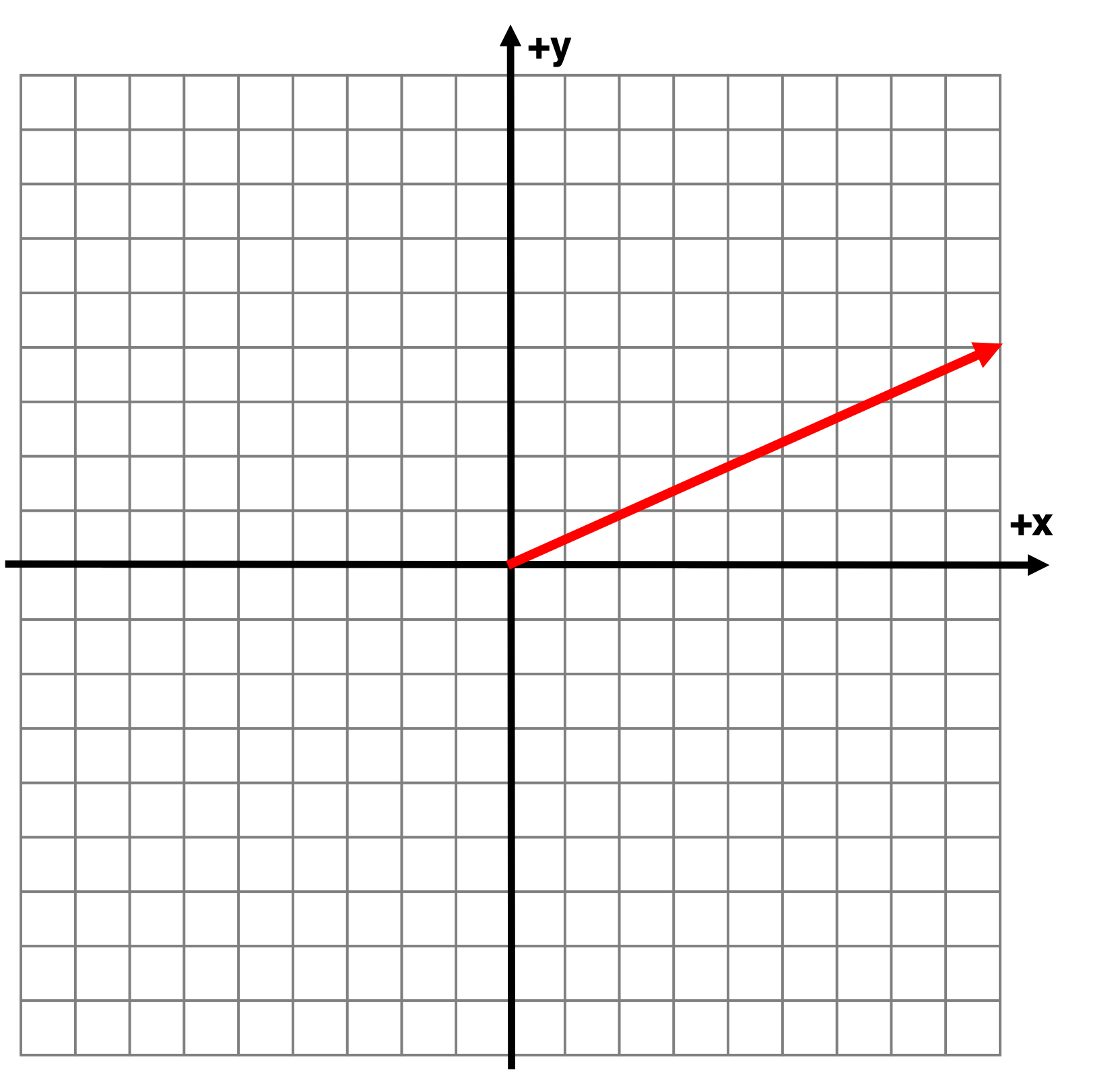
What is the Resultant?
Each square is 1 meter in length and width
9.85m
200
I walk 13 meters north, then 15 meters east, then turn back to north and walk another 10 meters.
What is my resultant displacement?
R = 27.5m
300
Displacement vector A has a magnitude of 48.6 meters and a direction of 21.1 degrees north of west. Determine the x- and y-components of vector A.
x= 45.3m
y=17.5m
300
A hiker takes a trip which consists of two segments. Path A is 48.5 km long heading 57.0 degrees N of East. Path B is 91.4 km long in a direction 21.2 degrees N of W. Complete the table below.
Ax= 26.4km Rx= 58.8km
Ay= 40.7km Ry= 73.8km
Bx= 33.1km R= 94.3km
By= 85.2km
300
If I row a boat perpendicular to the shore of a river Hoping to reach the other side. What will my velocity be if I row at a rate of 5 m/s east while the current of the river is 13 m/s? north?
14m
400
Displacement vector B has a magnitude of 53.4 meters and a direction of 55.3 degrees south of west. Determine the x- and y-components of vector B.
x= 30.4m
y= 43.9m
400
A hiker takes a trip which consists of three segments. Path A is 8.9 km long heading 57.0 degrees North of East. Path B is 10.6 km long in a direction due East. Path C is 3.1 km long heading 47.5 degrees East of South. Resolve each displacement vector into its components; consider using a table like the one below to organize your results.
3) Finally determine the magnitude and the direction of the resultant.
Ax= 4.8km Cx= 2.3km
Ay= 7.5km Cy= 2.1km
Bx= 10.6km Rx= 17.7km
By= 0 Ry= 5.4km
R= 18.5km Angle= 17 North of East
400
A boat heads due east directly across a 118.0 meter wide river. The water flows due south with a speed of 2.1 m/s with respect to the shore. The boat speed with respect to the water is 5.5 m/s.
1. Determine the resultant velocity
2. How long will it take him to reach the shore?
Resultant Velocity: 5.9m
Time to reach shore: 21.5s
400
A stone is thrown horizontally to the right at a speed of 18.9 m/s from the top of a cliff that is 90.2 m high.
How long does it take the stone to reach the bottom of the cliff?
How far from the base of the cliff does the stone hit the ground?
What is the horizontal component of the stone's velocity just before it hits the ground?
What is the vertical component of the stone's velocity just before it hits the ground?
t= 4.3s Vfx= 18.9m/s
Dx= 81.3m Vfy=42.14m/s
500
A spelunker (person who explores caves) determines that the cave entrance is located 334 meters, 249.3° CCE from her current position. Determine the components of this resultant vector.
x = 118.1m
y = 312.4m
500
Mia Ander exits the front door of her home and walks along the path shown in the diagram at the right (not to scale). The walk consists of four legs with the following magnitudes:
A = 85.0 meters
B = 262.2 meters
C = 140.9 meters
D = 176.4 meters
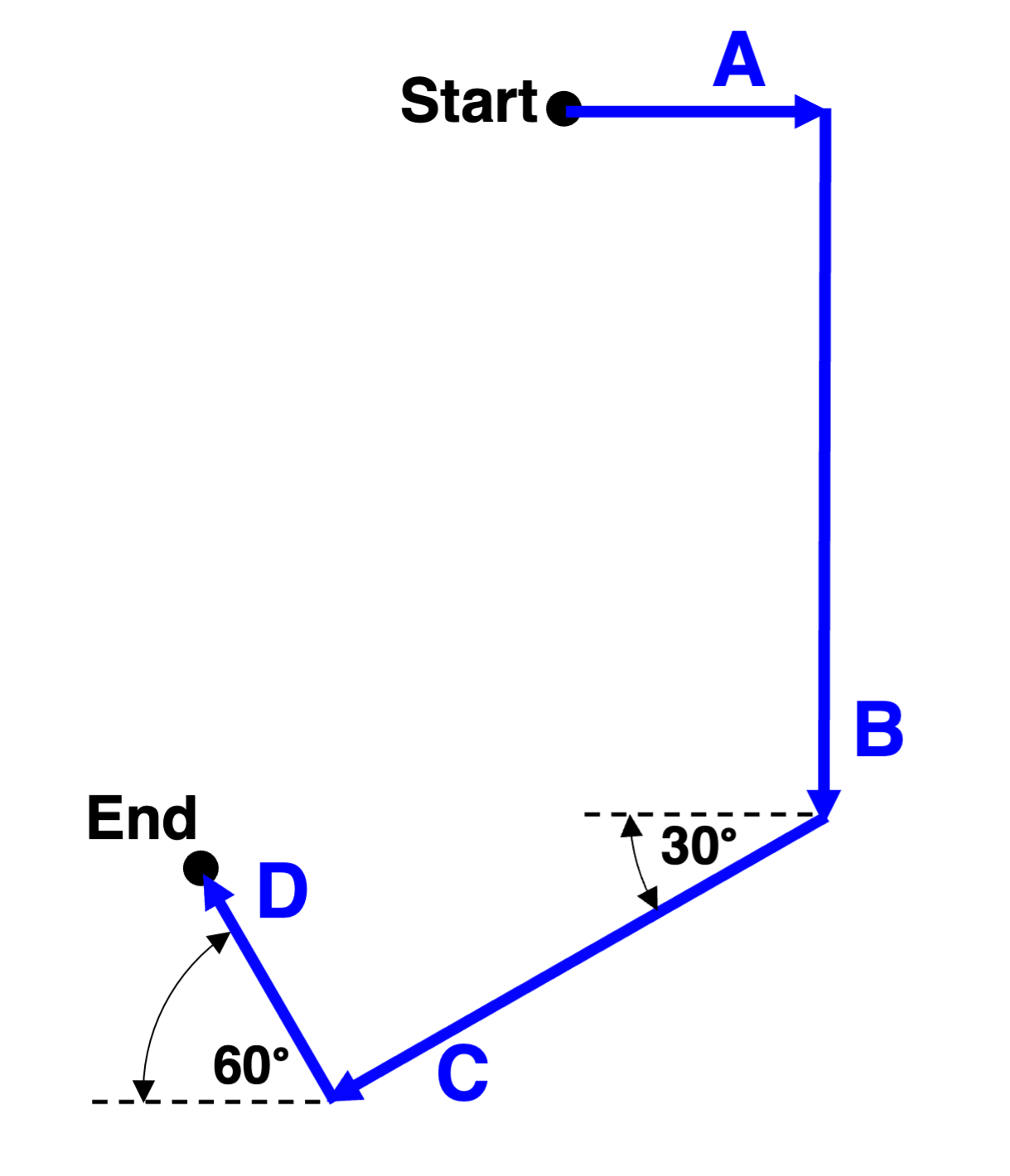
Ax= 85m Cx= 122m
Ay= 0m Cy= 70.4m
Bx= 0m Rx= 125.2m
By= 262.2m Ry= 179.6m
Dx=88.2m Dy=153m
R= 218.9km
Angle= 35 degrees south of west
500
Glenda and Harold are attempting to cross a river in a kayak. The river flows due east at 2.0 m/s. Glenda and Harold head the kayak due north and row at 2.5 m/s (relative to the water). The river is 40.9 m wide at this location.
1. Determine the magnitude of the resultant velocity of the kayak.
2. Determine the direction of the resultant velocity of the kayak relative to the shore.
3. Determine the time for Glenda and Harold to cross the river.
Velocity= 3.2m/s 39 degrees east of north
Time=16.36s
500
A Chicago Bear place kicker launches a kickoff at an angle of 32.4 degrees to the horizontal and a speed of 20.2 m/s.
Calculate the time for the football to rise to the highest point in the trajectory.
Calculate the total time the football is in the air.
Calculate the horizontal distance of the football.
Calculate the maximum height to which the football rises.
tup= 1.1s ttotal= 2.2s
Dx= 24.2m Dy= 6.2m